Суретте функцияның графигі көрсетілген \(\displaystyle y=f\left(x\right){\small.}\) Нүктелер \(\displaystyle -2{\small,}\, -1{\small,}\, 1{\small,}\, 2{\small}\) абсцисса осінде белгіленген. Белгіленген нүктелерді туындының мәннің кему ретімен орналастырыңыз.
\(\displaystyle -2{\small,}\, -1{\small,}\, 1{\small,}\, 2{\small}\) нүктелеріне жақын жерде функцияның әрекетін анықтайық.
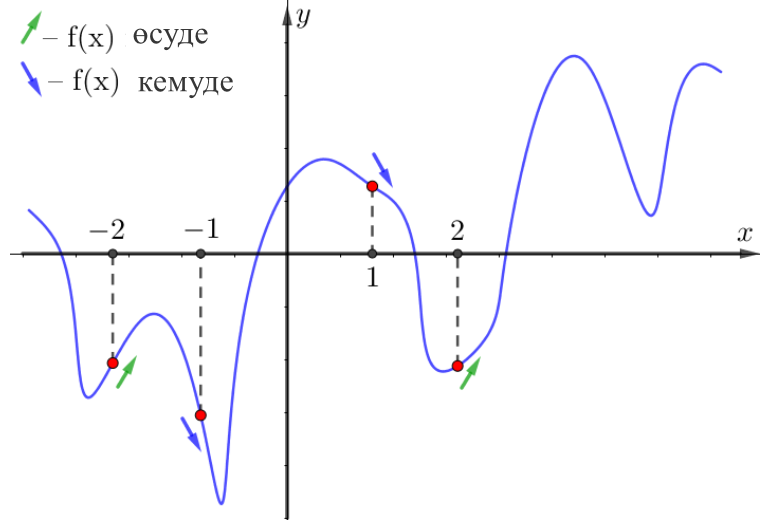
Аламыз:
| Нүкте | Маңайдағы функцияның әрекеті | Нүктедегі туындының мәні |
| \(\displaystyle -2,\, 2\) | \(\displaystyle f(x)\) артады | \(\displaystyle f^{\prime}(x)\ge0\) |
| \(\displaystyle -1, 1\) | \(\displaystyle f(x)\) кемуде | \(\displaystyle f^{\prime}(x)\le0\) |
Сонымен бірге белгіленген нүктелердің ешқайсысында \(\displaystyle \rm OX\) жанама оське параллель емес. Бұл кестедегі теңсіздік белгілері қатаң екенін білдіреді:
| Нүкте | Нүктедегі туындының мәні |
| \(\displaystyle -2,\, 2\) | \(\displaystyle f^{\prime}(x)>0\) |
| \(\displaystyle -1, 1\) | \(\displaystyle f^{\prime}(x)<0\) |
Яғни \(\displaystyle -2\) және \(\displaystyle 2\) нүктелеріндегі туындының мәндері \(\displaystyle -1\) және \(\displaystyle 1{\small}\) нүктелеріндегі туындының мәндерінен үлкен.
Алдымен \(\displaystyle -2{\small,}\) \(\displaystyle 2{ \small ,}\) нүктелеріндегі, содан кейін \(\displaystyle -1{\small,}\) \(\displaystyle 1{\small}\) нүктелеріндегі туынды мәндерін салыстырайық.
1. \(\displaystyle -2\) және \(\displaystyle 2{\small}\) нүктелерін қарастырыңыз.
\(\displaystyle x_0\) нүктесіндегі туындының мәні \(\displaystyle \tg(\alpha){ \small ,}\) мұндағы \(\displaystyle \alpha\) – қисықтағы сәйкес нүктедегі \(\displaystyle y=f(x){\small}\) жанаманың еңісі
Сондықтан \(\displaystyle -2\) және \(\displaystyle 2{ \small }\) нүктелеріндегі туындының мәнін салыстыру үшін мына ережені қолданамыз:
Егер \(\displaystyle \rm OX{\small}\) жанама осьтің оң бағытымен сүйір бұрыш түзсе, онда
көлбеу бұрышы неғұрлым үлкен болса, жанама соғұрлым үлкен болады.
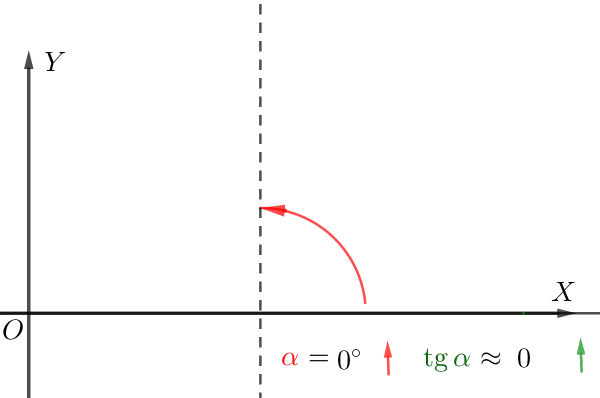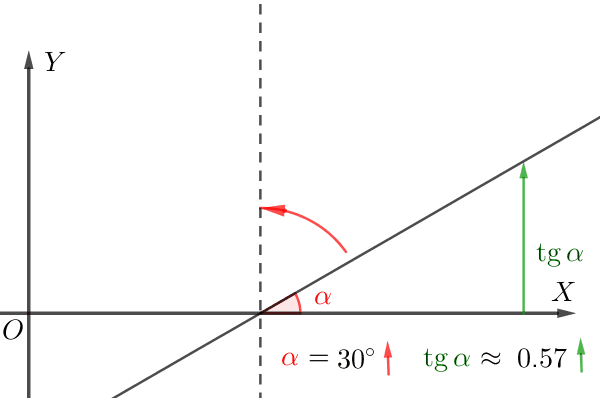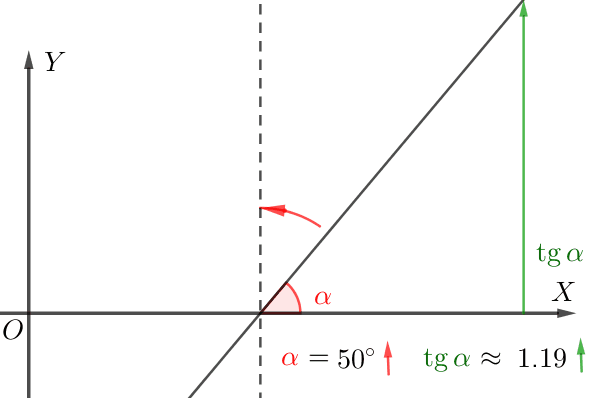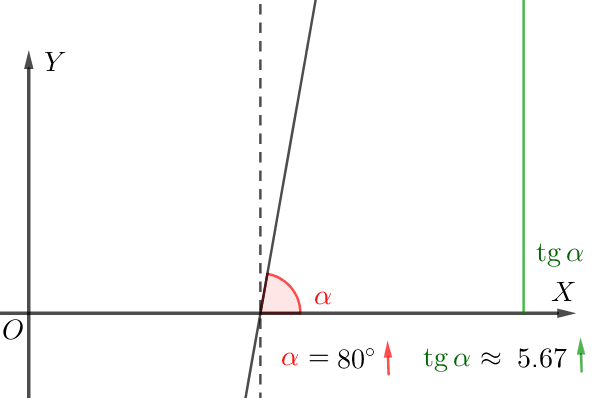
\(\displaystyle -2\) және \(\displaystyle 2{\small}\) нүктелеріндегі жанамаларды құрастырайық.
Суреттен тангенстің көлбеу бұрышы \(\displaystyle \color{green}{\alpha}\) жанаманың \(\displaystyle \color{red}{\beta}{\small}\) көлбеу бұрышынан үлкен екенін көруге болады.
Демек, бұрыштың тангенсі \(\displaystyle \color{green}{\alpha}\) бұрыштың жанамасынан \(\displaystyle \color{red}{\beta}{\small}\) үлкен.
Сәйкесінше туынды \(\displaystyle -2{\small }\) нүктесінде үлкен болады.
\(\displaystyle f^{\prime}(-2)>f^{\prime}(2)>0{\small.}\)
2. \(\displaystyle -1\) және \(\displaystyle 1{\small}\) нүктелерін қарастырыңыз.
\(\displaystyle -1\) және \(\displaystyle 1{ \small}\) нүктелеріндегі туындының мәнін салыстыру үшін мына ережені қолданамыз:
Егер \(\displaystyle \rm OX{\small}\) жанама осьтің оң бағытымен доғал бұрыш түзсе, онда
көлбеу бұрышы неғұрлым аз болса, жанама соғұрлым аз болады.
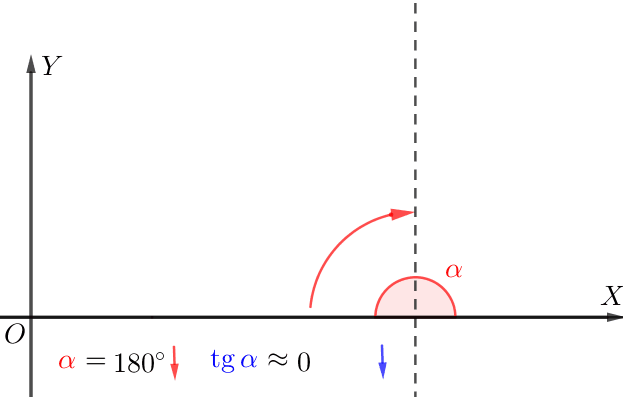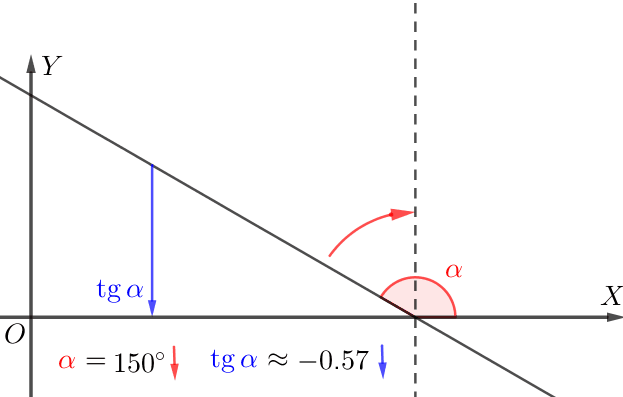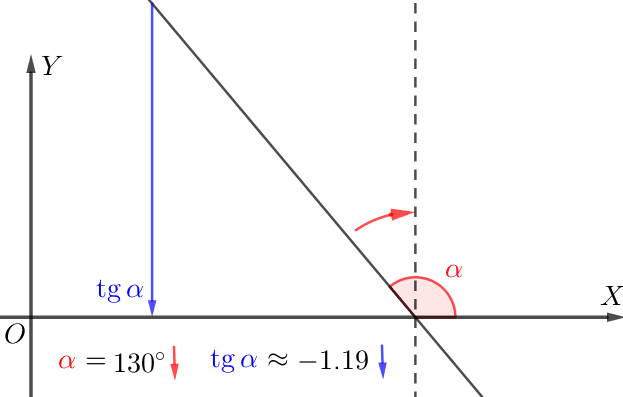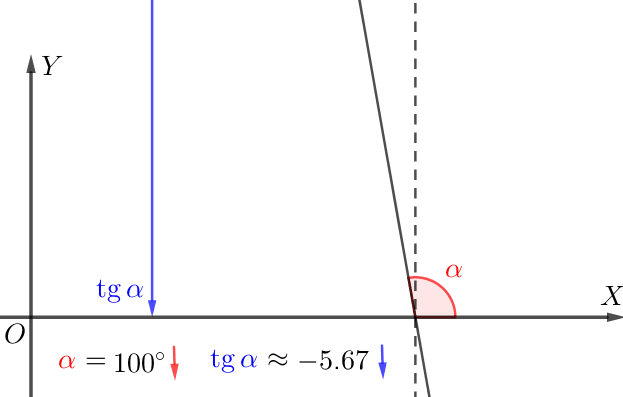
\(\displaystyle -1\) және \(\displaystyle 1{\small}\) нүктелеріндегі жанамаларды құрастырайық.
Тангенс бұрышын \(\displaystyle \color{#7F00FF}{\gamma}\) және жанама бұрышын ( дельта . ) салыстырыңыз
\(\displaystyle -1\) кезінде жанама \(\displaystyle 1 {\small}\) кезіндегі жанамаға қарағанда "тік" (кемірек көлбеу) болады.
Сондықтан тангенстің еңісі \(\displaystyle \color{#7F00FF}{\gamma}\) жанаманың еңісінен ( дельта) кіші \(\displaystyle \delta{\small.}\)
Бұл, \(\displaystyle \tg\color{#7F00FF}{\gamma}\) мәнінен \(\displaystyle \tg\delta\) кіші екенін және сәйкесінше туындының \(\displaystyle -1{\small}\) нүктесінде аз екенін білдіреді.
\(\displaystyle f^{\prime}(-1)<f^{\prime}(1)<0{\small.}\)
Осылайша, біз аламыз:
\(\displaystyle f^{\prime}(-2)>f^{\prime}(2)>0>f^{\prime}(1)>f^{\prime}(-1){\small.}\)
Сонымен, кему ретімен туынды нүктенің мәндері:
\(\displaystyle -2,\,2,\,1,\,-1{\small.}\)