Суретте функцияның графигі көрсетілген \(\displaystyle y = f(x){\small }\) х осінде жеті нүкте белгіленген: :\(\displaystyle x_1,\, x_2,\, x_3,\, x_4,\, x_5,\, x_6,\, x_7{\small .}\) Қалай осы нүктелердің көбі функциясының туындысы \(\displaystyle f(x)\) оң?
Функцияның төмендеуі, артуы және туындының белгісі
\(\displaystyle f(x)\) аралықтағы \(\displaystyle (\alpha;\, \beta)\) функциясы арта түссе, онда кез келген \(\displaystyle x_0 \in (\alpha;\, \beta)\) үшін
\(\displaystyle f^{\prime}(x_0)\geqslant 0{ \small ,}\) егер \(\displaystyle f^{\prime}(x_0)\) бар болса.
\(\displaystyle f(x)\) аралықтағы \(\displaystyle (\alpha;\, \beta)\) функциясы төмендесе, онда кез келген \(\displaystyle x_0 \in (\alpha;\, \beta)\) үшін
\(\displaystyle f^{\prime}(x_0) \leqslant 0{ \small ,}\) егер \(\displaystyle f^{\prime}(x_0)\) бар болса.
\(\displaystyle x_1,\, x_2,\, x_3,\, x_4,\, x_5,\, x_6,\, x_7{\small}\) нүктелеріне жақын жерде функцияның әрекетін қарастырыңыз.
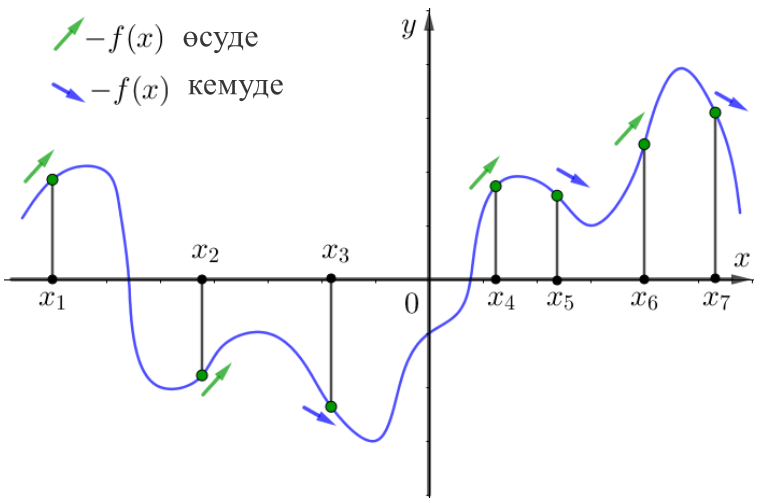
Аламыз:
| Нүкте | Функцияның нүктенің маңайындағы әрекеті | Нүктедегі туынды белгі |
| \(\displaystyle x_1,x_2, x_4, x_6\) | \(\displaystyle f(x)\) өсуде\(\displaystyle \color{green}{\nearrow}\) | \(\displaystyle f^{\prime}(x)\ge 0\) |
| \(\displaystyle x_3, x_5, x_7\) | \(\displaystyle f(x)\) кемуде\(\displaystyle \color{blue}{\searrow}\) | \(\displaystyle f^{\prime}(x) \le 0\) |
Таңдалған нүктелердің ешқайсысында \(\displaystyle \rm OX{\small}\) жанама оське параллель емес. Демек, бұл нүктелердің барлығында туынды нөлге тең емес.
Яғни, кестеде барлық теңсіздік белгілері қатаң:
| Нүкте | Нүктедегі туынды белгі |
| \(\displaystyle x_1,x_2, x_4, x_6\) | \(\displaystyle f^{\prime}(x)> 0\) |
| \(\displaystyle x_3, x_5, x_7\) | \(\displaystyle f^{\prime}(x) < 0\) |
Сондықтан туынды төрт нүктеде оң болады.
Жауабы: \(\displaystyle 4{\small.}\)