Найдите значение выражения:
\(\displaystyle \frac{4 \cos 146^\circ}{\cos 34^ \circ}=\)
В данном выражении \(\displaystyle \frac{4 \cos 146^\circ}{\cos 34^ \circ}\) два разных угла.
Найдем между ними взаимосвязь: у них может быть хорошая сумма или хорошая разность (то есть равная \(\displaystyle 90^ \circ\), \(\displaystyle 180^ \circ\), \(\displaystyle 270^ \circ\), \(\displaystyle 360^ \circ\) и т.п.).
В нашем случае у углов хорошая сумма: \(\displaystyle 146^ \circ+34^ \circ=\color{blue}{180^ \circ}{\small .}\)
Отсюда: \(\displaystyle \color{blue}{146^ \circ=180^ \circ-34^ \circ} {\small .}\)
Тогда
\(\displaystyle \frac{4 \cos \color{blue}{146^\circ}}{\cos 34^ \circ}=\frac{4 \cos (\color{blue}{180^\circ-34^\circ})}{\cos 34^ \circ}{\small .}\)
Получилась формула приведения. Применим ее.
1) Определим, в какой четверти находится угол \(\displaystyle 180^\circ-34^\circ :\)
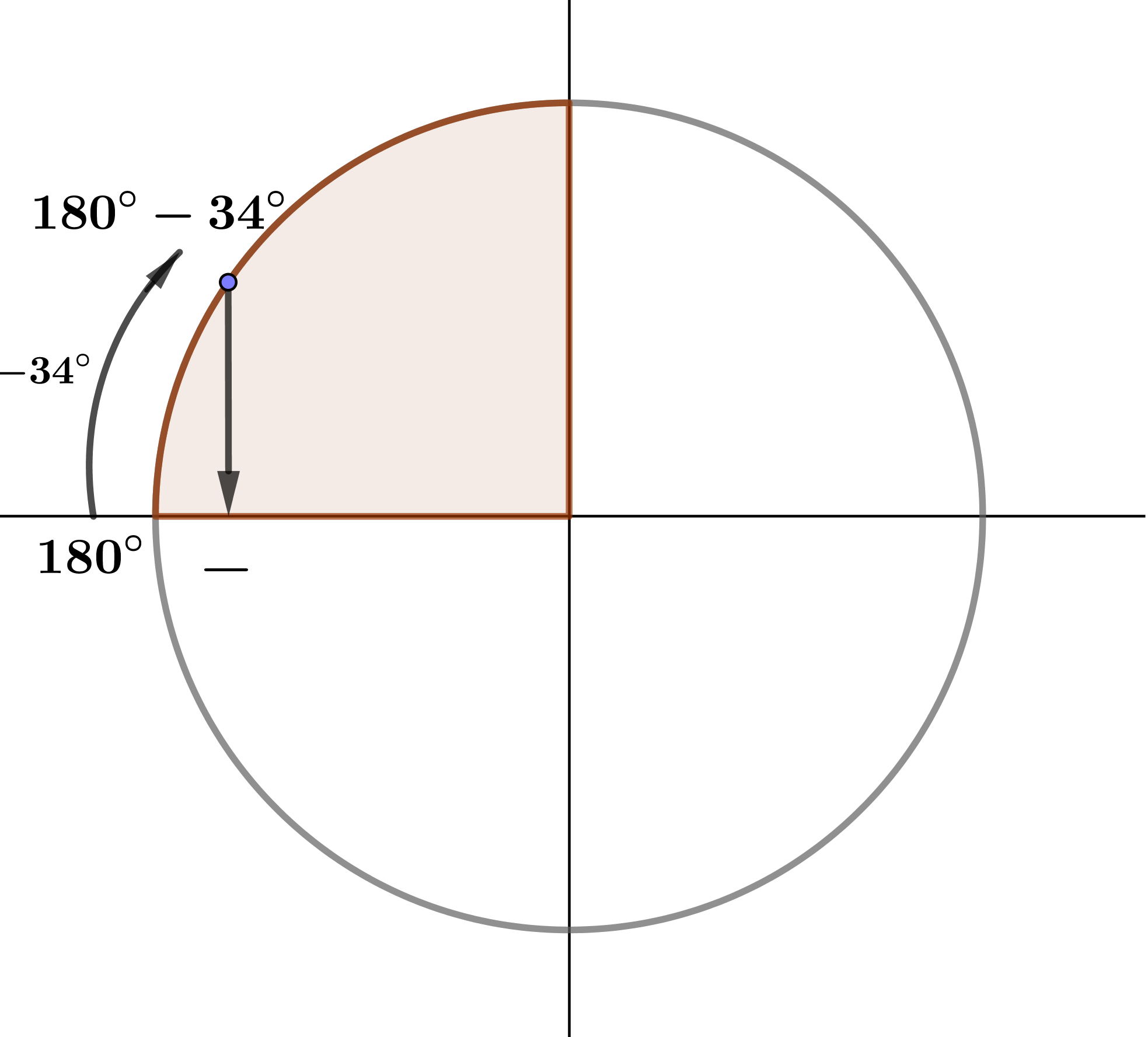
Значит, угол \(\displaystyle 180^\circ-34^\circ \) находится во второй четверти.
2) Определим знак исходной функции.
Во второй четверти косинус отрицательный (\(\displaystyle {\bf -}\)).
3) Определим, какая будет функция.
Так как к аргументу \(\displaystyle -34^\circ\) прибавляем \(\displaystyle 180^\circ ,\) то функция не меняется.
Значит,
\(\displaystyle \cos (180^\circ-34^\circ)=-\cos34^\circ {\small .}\)
Получаем:
\(\displaystyle \frac{4 \color{blue}{\cos (180^\circ-34^\circ)}}{\cos 34^ \circ}=\frac{4 (\color{blue}{-\cos 34^\circ})}{\cos 34^ \circ}=\frac{-4 \cos 34^\circ}{\cos 34^ \circ}{\small .}\)
Сократим дробь на \(\displaystyle \cos 34^ \circ \) и получим ответ:
\(\displaystyle \frac{-4 \cos 34^\circ}{\phantom1 \cos 34^ \circ}=-4{\small .}\)
Таким образом, верна следующая цепочка равенств:
\(\displaystyle \frac{4 \cos 146^\circ}{\cos 34^ \circ}=\frac{4 \cos (180^\circ-34^\circ)}{\cos 34^ \circ}=\frac{-4 \cos 34^\circ}{\phantom1 \cos 34^ \circ}=-4{\small .}\)
Ответ: \(\displaystyle -4 {\small.} \)