Өрнектің мәнін табыңыз:
\(\displaystyle \frac{4 \cos 146^\circ}{\cos 34^ \circ}=\)
Берілген \(\displaystyle \frac{4 \cos 146^\circ}{\cos 34^ \circ}\) өрнегінде екі түрлі бұрыш бар.
Олардың арасындағы байланысты табамыз: оларда жақсы қосынды немесе жақсы айырмашылық болуы мүмкін (яғни \(\displaystyle 90^ \circ,\) \(\displaystyle 180^ \circ,\) \(\displaystyle 270^ \circ,\) \(\displaystyle 360^ \circ\) және т.б. тең).
Біздің жағдайда бұрыштарда жақсы қосынды бар: \(\displaystyle 146^ \circ+34^ \circ=\color{blue}{180^ \circ}{\small .}\)
Осыдан: \(\displaystyle \color{blue}{146^ \circ=180^ \circ-34^ \circ} {\small .}\)
Сонда
\(\displaystyle \frac{4 \cos \color{blue}{146^\circ}}{\cos 34^ \circ}=\frac{4 \cos (\color{blue}{180^\circ-34^\circ})}{\cos 34^ \circ}{\small .}\)
Келтіру формуласы болып шықты. Оны қолданамыз.
1) \(\displaystyle 180^\circ-34^\circ \) бұрышының қай ширекте екенін анықтайық:
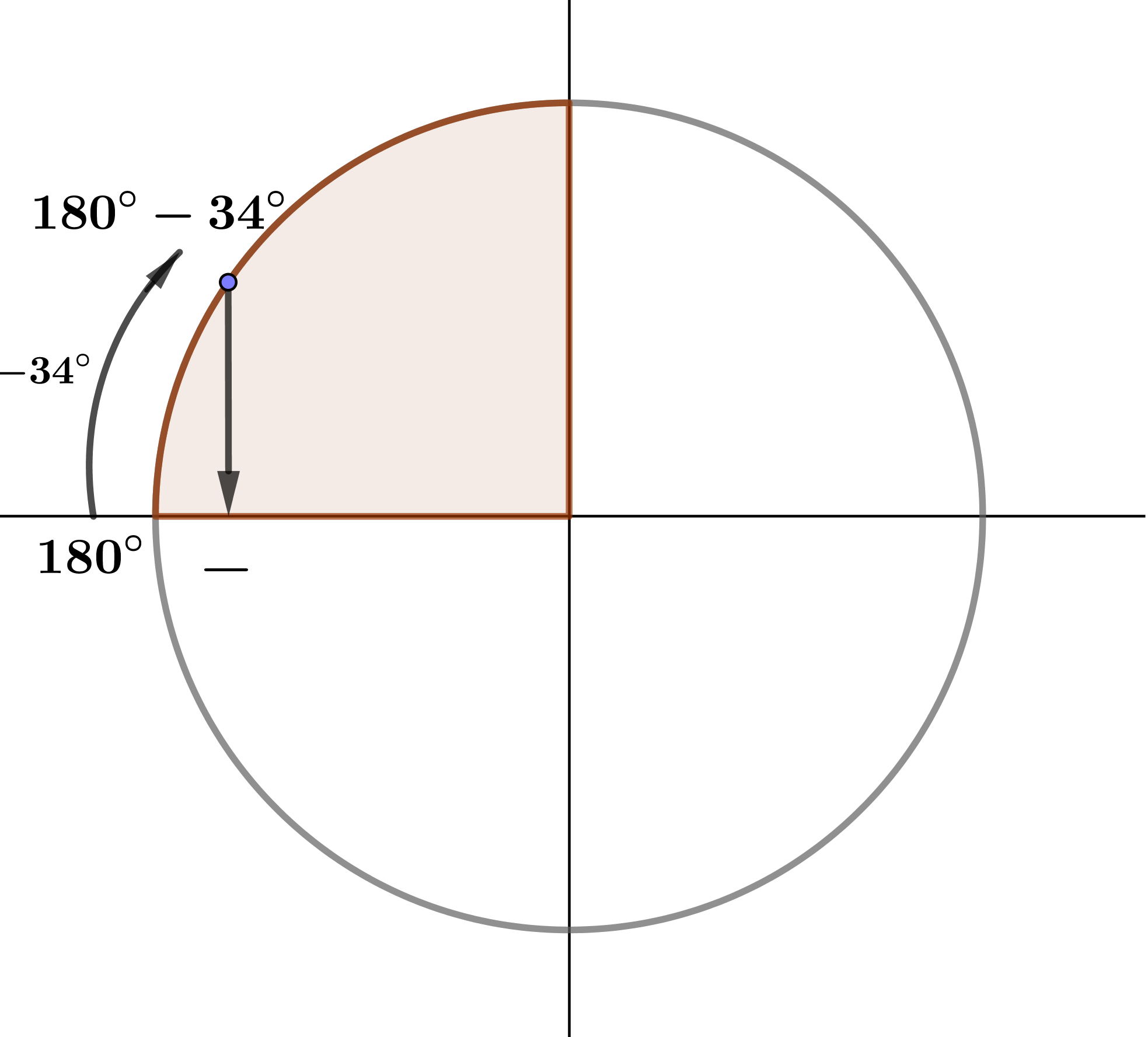
Демек, \(\displaystyle 180^\circ-34^\circ \) бұрышы екінші ширекте жатыр.
2) Бастапқы функцияның таңбасын анықтайық.
Екінші ширекте косинус теріс (\(\displaystyle {\bf -}\)).
3) Қандай функция болатынын анықтайық.
\(\displaystyle -34^\circ\) аргументіне \(\displaystyle 180^\circ \) қосылатындықтан, онда функция өзгермейді.
Демек,
\(\displaystyle \cos (180^\circ-34^\circ)=-\cos34^\circ {\small .}\)
Келесіні аламыз:
\(\displaystyle \frac{4 \color{blue}{\cos (180^\circ-34^\circ)}}{\cos 34^ \circ}=\frac{4 (\color{blue}{-\cos 34^\circ})}{\cos 34^ \circ}=\frac{-4 \cos 34^\circ}{\cos 34^ \circ}{\small .}\)
Бөлшекті \(\displaystyle \cos 34^ \circ \) қысқартып жауабын аламыз:
\(\displaystyle \frac{-4 \cos 34^\circ}{\phantom1 \cos 34^ \circ}=-4{\small .}\)
Осылайша, келесі теңдік тізбегі дұрыс:
\(\displaystyle \frac{4 \cos 146^\circ}{\cos 34^ \circ}=\frac{4 \cos (180^\circ-34^\circ)}{\cos 34^ \circ}=\frac{-4 \cos 34^\circ}{\phantom1 \cos 34^ \circ}=-4{\small .}\)
Жауабы: \(\displaystyle -4 {\small.} \)