Өрнектің мәнін табыңыз:
\(\displaystyle \frac{3\cos(\pi - \beta) + \sin(\frac{\pi}{2} + \beta)} { \cos(\beta + 3\pi)}=\)
Ережеге сәйкес келтіру формуласын қолданамыз:
1) \(\displaystyle \alpha \in \left(0;\frac{\pi}{2}\right){\small }\) екенін болжап, ширекті анықтаймыз.
2) Бастапқы функцияның таңбасын анықтаймыз.
3) Қандай функция болатынын анықтаймыз.
Егер \(\displaystyle \pm \alpha \) бұрышына келесілерді қосып немесе азайтсақ
- \(\displaystyle \pm\pi ,\, \pm 2\pi ,\, \pm 3\pi,\, \pm 4\pi,\,\ldots\) (\(\displaystyle \pi\) бүтін саны), онда функцияны өзгертпейміз;
- \(\displaystyle \pm\frac{\pi}{2},\, \pm\frac{3\pi}{2},\, \pm\frac{5\pi}{2},\, \pm\frac{7\pi}{2},\, \ldots\) (\(\displaystyle \pi\) жартыларының тақ саны), онда функцияны өзгертеміз: \(\displaystyle \sin\) \(\displaystyle \leftrightarrow\) \(\displaystyle \cos\) және \(\displaystyle \tg\) \(\displaystyle \leftrightarrow\) \(\displaystyle \ctg{\small .}\)
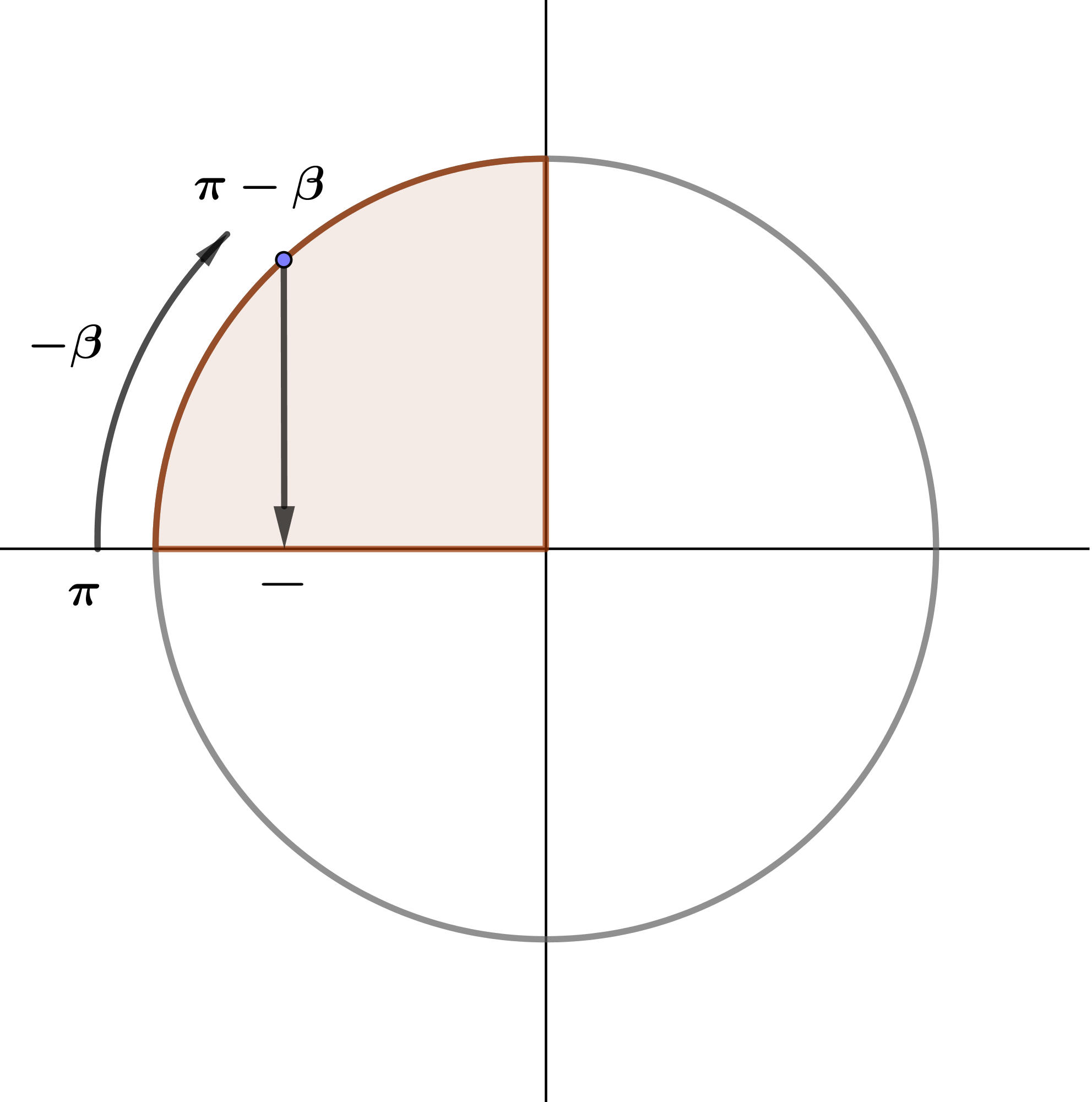
\(\displaystyle \cos(\pi - \beta)=-\cos\beta \)
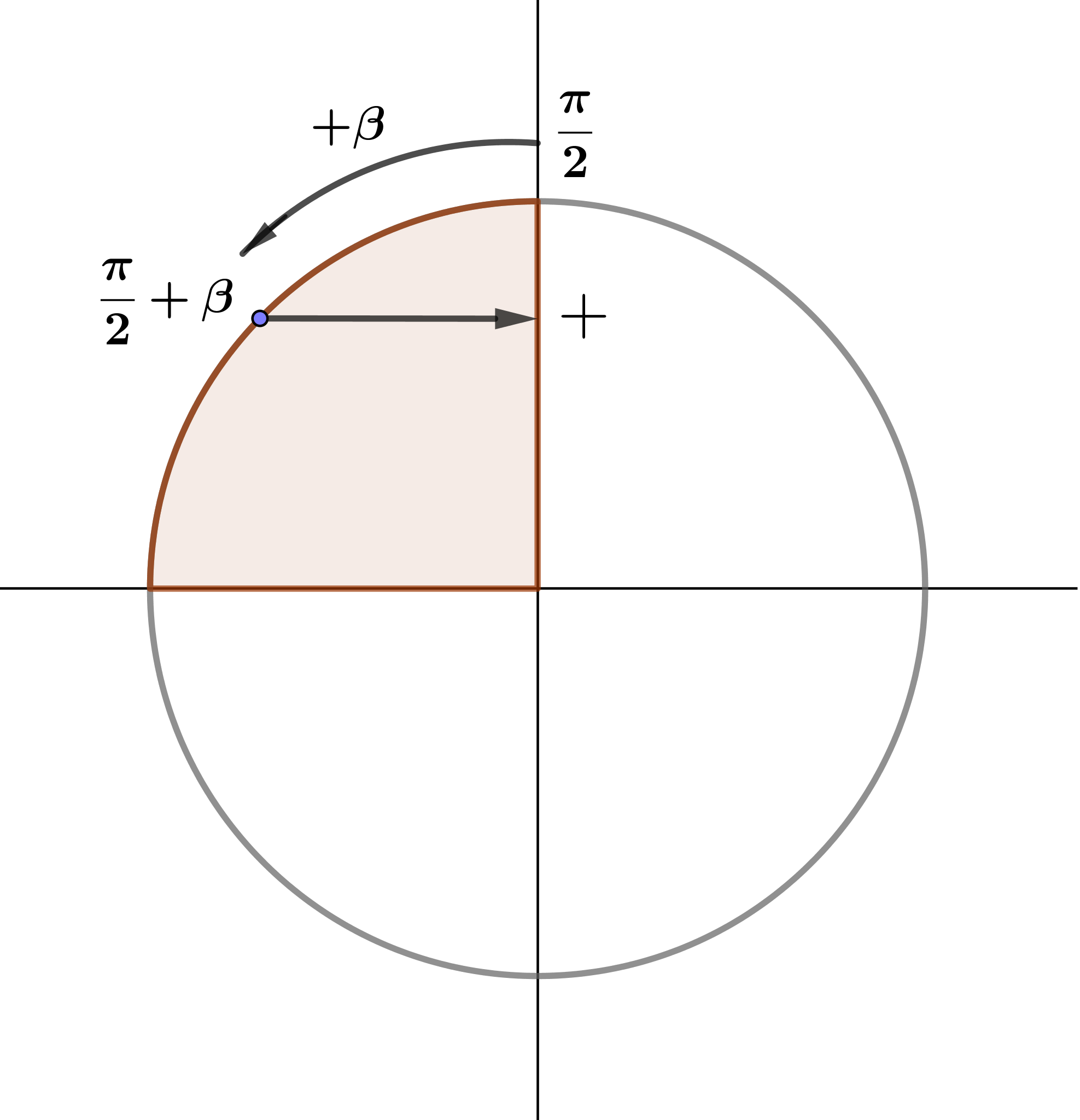
- \(\displaystyle \sin(\frac{\pi}{2} + \beta)=\cos\beta\)
- \(\displaystyle \cos(\beta + 3\pi)= \cos(3\pi+\beta)=-\cos\beta\)
Алынған нәтижелерді бастапқы өрнекке ауыстырайық:
\(\displaystyle \frac{3\color{blue}{\cos(\pi - \beta)} + \color{green}{\sin(\frac{\pi}{2} + \beta)}} { \color{orange}{\cos(\beta + 3\pi)}}=\frac{3(\color{blue}{-\cos \beta} )+ \color{green}{\cos\beta}} { \color{orange}{-\cos\beta}}=\frac{-3\cos \beta + \cos\beta} { -\cos\beta}{\small .}\)
Бөлшекті жеңілдетейік:
\(\displaystyle \frac{-3\cos \beta + \cos\beta} { -\cos\beta}=\frac{-2\cos \beta} { -\cos\beta}=2{\small .}\)
Жауабы: \(\displaystyle 2 {\small.} \)