Төмендегіге тең болатын тригонометриялық өрнекті таңдаңыз:
\(\displaystyle \cos\left(\frac{\pi}{2}-\alpha\right)=\)
Өрнектердің әрқайсысы
\(\displaystyle \sin\left(\frac{\pi}{2}\pm \alpha\right),\, \cos\left(\frac{\pi}{2}\pm \alpha\right), \sin\left(\frac{3\pi}{2}\pm \alpha\right),\, \cos\left(\frac{3\pi}{2}\pm \alpha\right),\, \sin\left(\alpha-\frac{\pi}{2}\right),\, \cos\left(\alpha-\frac{\pi}{2}\right)\)
\(\displaystyle \sin\left(\pi\pm \alpha\right),\, \cos\left(\pi\pm \alpha\right), \, \sin\left(\alpha-\pi \right),\, \cos\left(\alpha-\pi\right)\)
не \(\displaystyle \pm\sin\alpha{ \small ,}\) не \(\displaystyle \pm\cos\alpha{\small}\) тең.
- Егер формулада \(\displaystyle \frac{\pi}{2} \) немесе \(\displaystyle \frac{3\pi}{2} { \small}\) болса, онда синус косинусқа, ал косинус синусқа өзгереді, әйтпесе функция өзгермейді.
- Синус пен косинус белгісі бастапқы өрнектің белгісімен анықталады, егер бұрыш \(\displaystyle 0<\alpha<\frac{\pi}{2}{\small}\) болса.
\(\displaystyle \cos\left(\frac{\pi}{2}-\alpha\right)\) өрнегінде \(\displaystyle \frac{\pi}{2}{ \small}\) болғандықтан, онда
\(\displaystyle {\bf \cos}\left(\frac{\pi}{2}-\alpha\right)=\,?\,{\bf \sin}\alpha{\small .}\)
Әрі қарай, синустың алдында қандай белгі тұруы керек екенін анықтаймыз.
Әрқашан \(\displaystyle \alpha\) бұрышы тригонометриялық шеңбердің бірінші ширегінде орналасқан деп санауға болады:
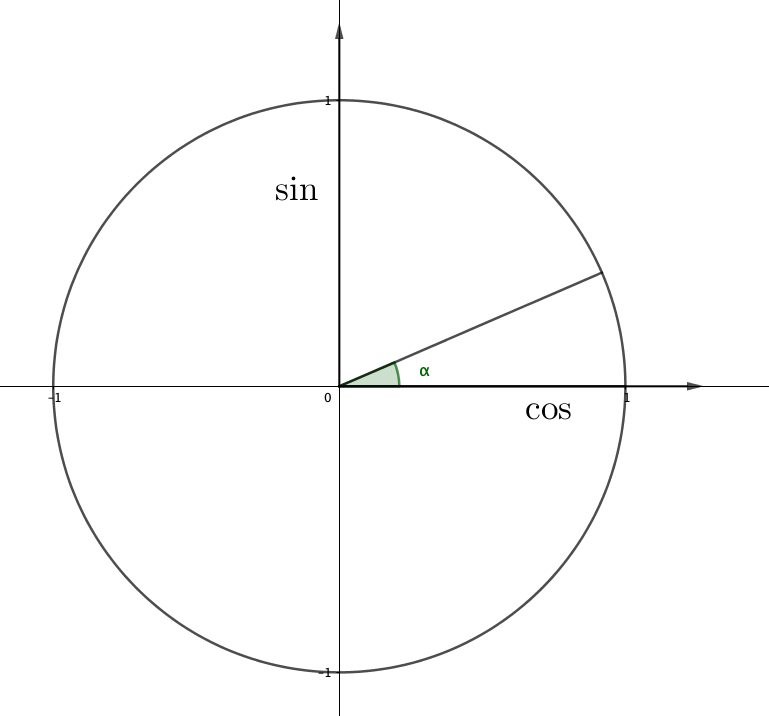
Онда \(\displaystyle \frac{\pi}{2}-\alpha\) бұрышы – бұл \(\displaystyle \alpha \) бұрышын \(\displaystyle \frac{\pi}{2}{\small}\) бұрышынан азайту арқылы алынған бұрыш.
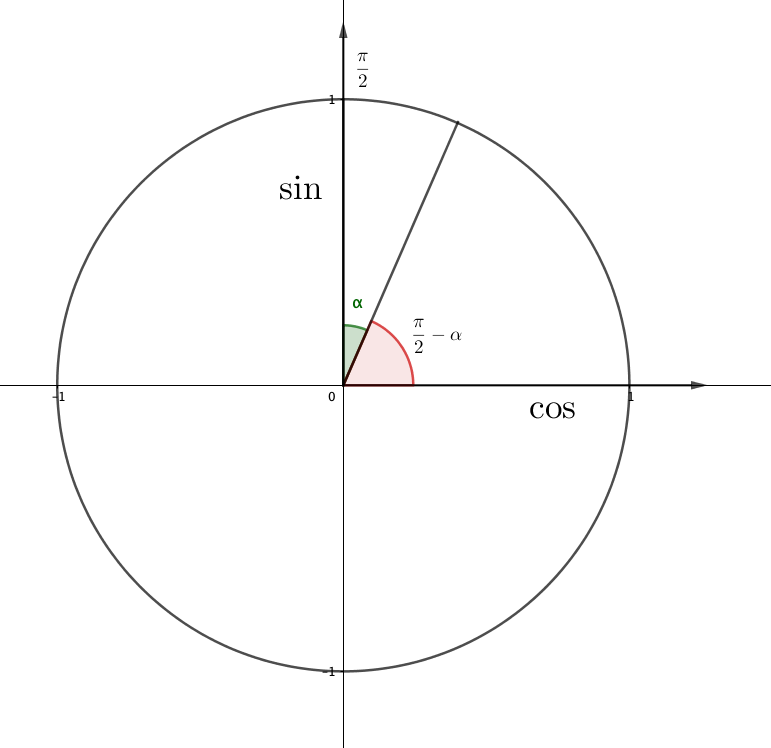
Бастапқы өрнектің таңбасын, анықтаймыз, яғни \(\displaystyle \cos\left(\frac{\pi}{2}-\alpha\right){\small}\) таңбасын:
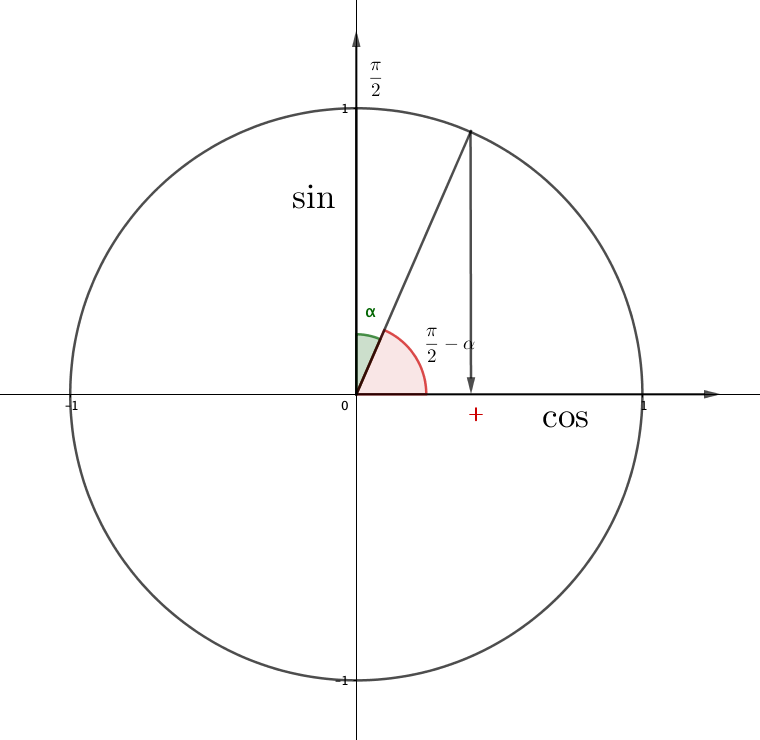
Плюс таңбасы. Демек,
\(\displaystyle \cos\left(\frac{\pi}{2}-\alpha\right)=\color{red}{+}\sin{\alpha}\)
немесе
\(\displaystyle \cos\left(\frac{\pi}{2}-\alpha\right)=\sin{\alpha}{\small .}\)
Жауабы: \(\displaystyle \cos\left(\frac{\pi}{2}-\alpha\right)=\sin{\alpha}{\small .}\)
Айырма косинусы формуласын қолданамыз.
Екі \(\displaystyle x\) және \(\displaystyle y\) бұрыштары үшін келесі дұрыс
\(\displaystyle \cos(x-y)=\cos x\cdot \cos y+\sin x\cdot \sin y{\small .}\)
Сонда
\(\displaystyle \cos\left(\frac{\pi}{2}-\alpha\right)=\cos\frac{\pi}{2}\cdot \cos\alpha+\sin\frac{\pi}{2}\cdot \sin\alpha{\small .}\)
\(\displaystyle \cos\frac{\pi}{2}=0\) және \(\displaystyle \sin\frac{\pi}{2}=1{ \small}\) болғандықтан төмендегіні аламыз:
\(\displaystyle \cos\left(\frac{\pi}{2}-\alpha\right)=0\cdot \cos\alpha+1\cdot \sin\alpha{ \small ,}\)
\(\displaystyle \cos\left(\frac{\pi}{2}-\alpha\right)=\sin\alpha{\small .}\)
Жауабы: \(\displaystyle \cos\left(\frac{\pi}{2}-\alpha\right)=\sin\alpha{\small .}\)