Ромбтың қабырғасы \(\displaystyle 5{\small}\) тең. Оның диагональдарының бірі екіншісінен \(\displaystyle 2\) үлкен. Кіші диагональды табыңыз.

\(\displaystyle BD=x\) – ромбтың кіші диагоналы болсын, демек \(\displaystyle AC=x+2 \) – ромбтың үлкен диагоналы.

Параллелограммның қасиеті бойынша диагональдар қиылысу нүктесімен екіге бөлінеді. Яғни,
\(\displaystyle BO=OD=\frac{x}{2}\) және \(\displaystyle AO=OC=\frac{x+2}{2}{\small.}\)
Ромбтың қасиеті бойынша диагональдар перпендикуляр. Яғни \(\displaystyle AOB\) бұрышы - тік.
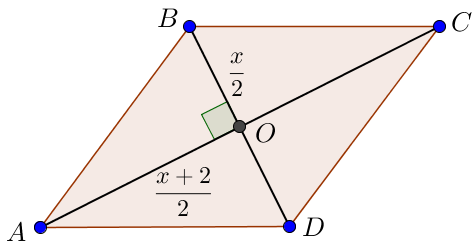
Тік бұрышты \(\displaystyle AOB{\small}\) үшбұрышынан ромбтың \(\displaystyle AB\) қабырғасын өрнектейік. Пифагор теоремасы бойынша
\(\displaystyle AB^2=AO^2+OB^2{\small.}\)
Демек
\(\displaystyle {5}^2=\left(\frac{x+2}{2}\right)^2+\left(\frac{x}{2}\right)^2{\small,}\)
\(\displaystyle 25=\frac{x^2+4x+4}{4}+\frac{x^2}{4}{\small,}\)
\(\displaystyle 100=2x^2+4x+4{\small,}\)
\(\displaystyle 2x^2+4x-96=0{\small,}\)
\(\displaystyle x^2+2x-48=0{\small.}\)
Квадрат теңдеуді шешейік.
Кесіндінің ұзындығы оң болғандықтан, онда \(\displaystyle x=6.\) Демек, ромбтың кіші диагоналінің ұзындығы \(\displaystyle 6{\small}\) тең
Жауабы: \(\displaystyle 6{\small .}\)