Задание
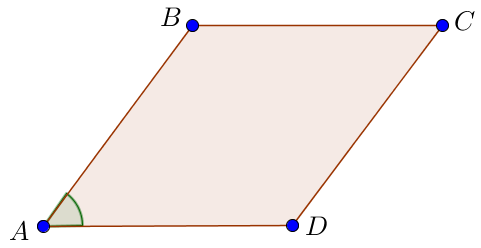
Острый угол ромба равен \(\displaystyle 70^\circ \small.\) Найдите угол между большей диагональю и стороной ромба. Ответ дайте в градусах.
Решение

Пусть \(\displaystyle \angle DAB = 70^{\circ}\) – острый угол ромба.
Большая диагональ ромба лежит против тупого угла.
Значит, нужно найти угол между диагональю \(\displaystyle AC\) и стороной ромба.
Диагонали ромба являются биссектрисами его углов.
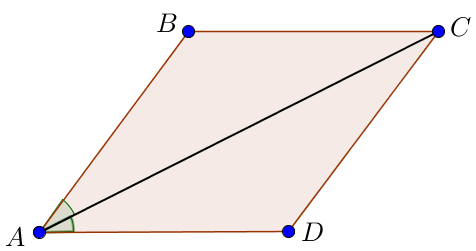
Тогда
\(\displaystyle \angle BAC = \angle DAC = \frac{1}{2}\cdot \angle DAB=\frac{1}{2} \cdot 70^{\circ} =35^{\circ} \small.\)
Поэтому искомый угол равен \(\displaystyle 35^\circ {\small .}\)
Ответ: \(\displaystyle 35 {\small .}\)