Ромбтың диагоналы \(\displaystyle 12\small,\) ромбтың қабырғасы \(\displaystyle 10 \small.\) Басқа диагоналының ұзындығын табыңыз.

\(\displaystyle O\) диагональ берілген \(\displaystyle BD=12\) ромбының диагональдарының қиылысу нүктесі \(\displaystyle ABCD \small\) болсын.

Параллелограмның қасиетіне сәйкес диагональдар қиылысу нүктесіне қарай екіге бөлінеді. білдіреді,
\(\displaystyle AO=OC\) және \(\displaystyle BO=OD=6 \small.\)
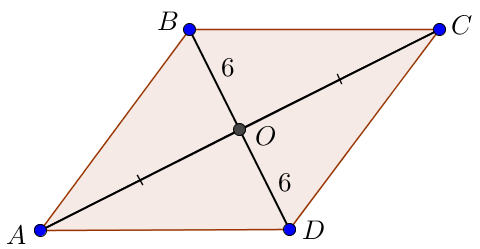
Ромбтың қасиеті бойынша диагональдары перпендикуляр. Сонымен бұрыш \(\displaystyle AOB\) – тік бұрыш болады.
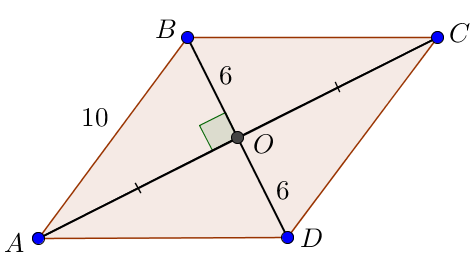
Тікбұрышты үшбұрышты қарастырайық \(\displaystyle AOB \small.\) Біз қабырғаларын білеміз \(\displaystyle AB=10\) және \(\displaystyle BO=6 \small.\) Қабырғасын \(\displaystyle AO \small\) табыңыз.
Пифагор теоремасы бойынша
\(\displaystyle AO^2=AB^2-OB^2 \small.\)
Содан кейін
\(\displaystyle AO^2=10^2-6^2=100-36=64\small.\)
Сегменттің ұзындығы оң болғандықтан \(\displaystyle AO=8 \small.\)
Сонымен , \(\displaystyle AC=2\cdot AO=16 {\small .}\)
Жауабы: \(\displaystyle 16 {\small .}\)