Ромбта \(\displaystyle ABCD\) қабырғасы \(\displaystyle 4 \small\) бұрышы \(\displaystyle BAD\) \(\displaystyle 60^\circ \small.\) Ромбтың \(\displaystyle BD\) диагоналін табыңыз.

Үшбұрышты қарастырайық \(\displaystyle BAD \small. \)
Ромбтың қабырғалары тең болғандықтан \(\displaystyle AB = AD \small.\) Сонда үшбұрыш \(\displaystyle BAD \) – тең қабырғалы, ал төбесіндегі бұрыш \(\displaystyle \angle BAD = 60^{\circ} \small.\)
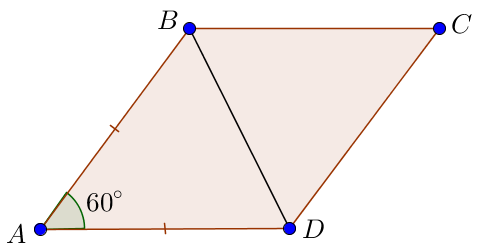
Тең қабырғалы үшбұрышта табанындағы бұрыштар тең:
\(\displaystyle \angle ADB = \angle ABD \small.\)
Үшбұрыштың бұрыштарының қосындысы \(\displaystyle 180^{\circ} \small,\) болғандықтан
\(\displaystyle \angle ADB = \angle ABD =\frac{180^{\circ} - \angle BAD}{2}= \frac{180^{\circ} - 60^{\circ}}{2}= \frac{120^{\circ}}{2}= 60^{\circ} \small.\)
Біз үшбұрыштың \(\displaystyle BAD \) барлық бұрыштары тең \(\displaystyle 60^{\circ} \small. \)
Сонымен үшбұрыш \(\displaystyle BAD \) – тең қабырғалы. Демек, \(\displaystyle BD = 4 \small.\)
Жауабы: \(\displaystyle 4 {\small .}\)