Тіктөртбұрыштың қабырғасы оның диагоналына \(\displaystyle 4:5\) және екінші қабырғасы \(\displaystyle 6\) тең тіктөртбұрыштың ауданын табыңыз.
\(\displaystyle AB=6\) және \(\displaystyle BC:AC=4:5\) болсын. Бұл \(\displaystyle BC\) кесіндісін \(\displaystyle 4\) тең бөлікке бөлсек \(\displaystyle AC\) кесіндісін \(\displaystyle 5\) тең бөлікке бөлуге болатынын білдіреді.
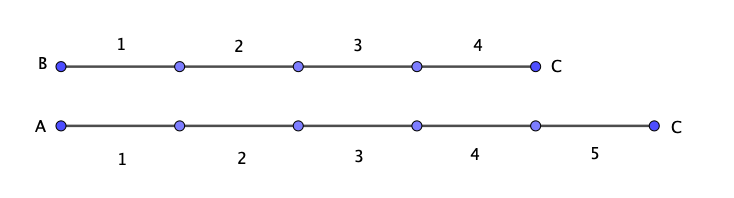
Бір бөліктің ұзындығын \(\displaystyle x\) арқылы белгілеңіз. Сонда \(\displaystyle BC=4x,\) ал \(\displaystyle AC=5x.\)
Үшбұрышты қарастырайық \(\displaystyle ABC.\) Өйткені \(\displaystyle \angle ABC = 90^{\circ},\) онда \(\displaystyle ABC\) – гипотенузасы \(\displaystyle A.\) тікбұрышты үшбұрыш болады.
Пифагор теоремасы бойынша \(\displaystyle AC^2=AB^2 + BC^2{\small.}\)
Демек,
\(\displaystyle (5x)^2=6^2 + (4x)^2,\)
\(\displaystyle 25x^2=36 + 16x^2,\)
\(\displaystyle 25x^2-16x^2=36,\)
\(\displaystyle 9x^2=36 \, | :\color{red}{9},\)
\(\displaystyle x^2=4.\)
Кесіндінің ұзындығы оң болғандықтан \(\displaystyle x=2.\)
Сонда \(\displaystyle BC=4x=8.\)
Тіктөртбұрыштың ауданы формуламен есептелетіндіктен \(\displaystyle S=AB\cdot BC,\) онда
\(\displaystyle S=6\cdot 8=48.\)
Жауабы: \(\displaystyle 48{\small .}\)