Үшбұрышта \(\displaystyle ABC\) бұрыш \(\displaystyle C\) \(\displaystyle 90^{\circ}{\small , }\) \(\displaystyle CB=8\) және \(\displaystyle \sin\angle A=0{,}5{\small .}\)
кесіндінің \(\displaystyle HB{\small }\) ұзындығын табыңыз
Тікбұрышты үшбұрыштың сүйір бұрыштарының қосындысы \(\displaystyle 90^{\circ} \small, \) болғандықтан \(\displaystyle \angle A +\angle B =90^{ \circ} \small.\) Содан кейін \(\displaystyle \sin \angle A = \sin(90^{\circ}-\angle B)=\cos \angle B \small.\) | 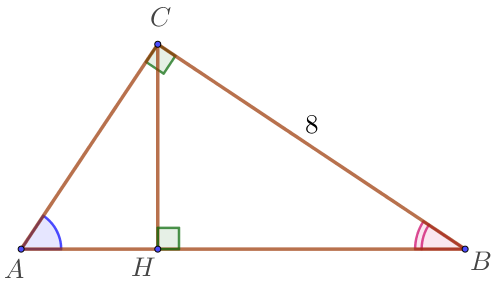 |
Тікбұрышты үшбұрышты \(\displaystyle CBH\small\) қарастырайық
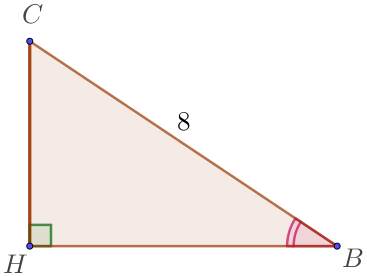 | Косинус анықтамасы бойынша \(\displaystyle \cos \angle B =\frac{BH}{CB}\small. \) Яғни \(\displaystyle 0{,}5=\frac{BH}{8} \small, \) \(\displaystyle BH=0{,}5 \cdot 8 \small, \) \(\displaystyle BH=4 \small. \) |
Жауабы: \(\displaystyle 4 \small. \)