Үшбұрышта \(\displaystyle ABC\) бұрыш \(\displaystyle C\) \(\displaystyle 90^{\circ},\) қабырға ұзындығы \(\displaystyle AB=5,\) \(\displaystyle \sin A=\frac{7}{25}.\)
Қабырғасының \(\displaystyle AC\small \) ұзындығын табыңыз
Анықтама бойынша
\(\displaystyle \sin A=\frac{CB}{AB}{\small .} \)
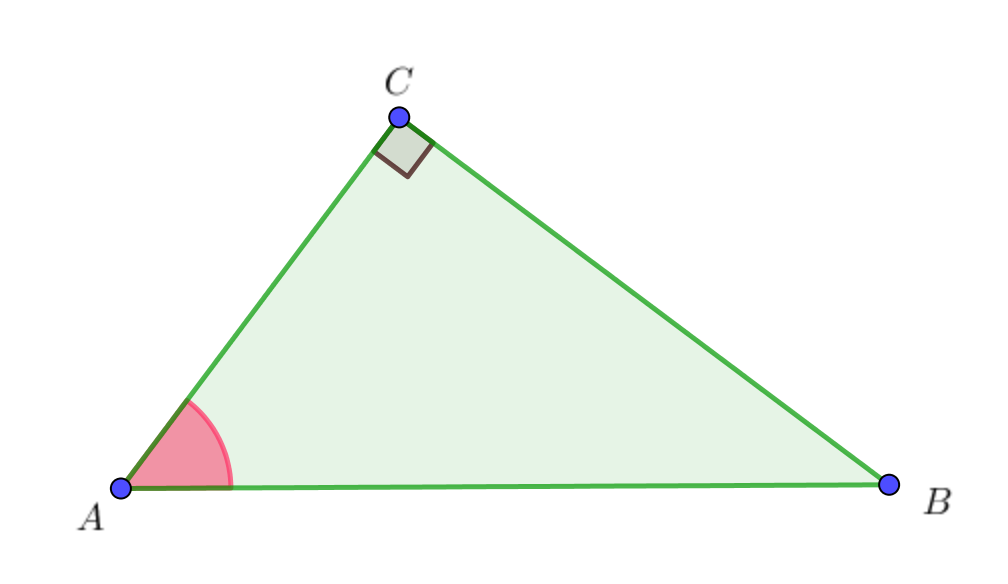
Белгілі мәндерді ауыстырыңыз \(\displaystyle AB=5{\small , }\) \(\displaystyle \sin A =\frac{7}{25}: \)
\(\displaystyle \frac{7}{25}=\frac{CB}{5}{\small .}\)
Осы жерден
\(\displaystyle CB=5\cdot \frac{7}{25}=\frac{7}{5}{\small .}\)
Пифагор теоремасы бойынша \(\displaystyle AC^2+CB^2=AB^2{\small .}\) Сонда
\(\displaystyle AC^2+\left(\frac{7}{5}\right)^2=5^2{\small .}\)
Осы жерден
\(\displaystyle AC^2=5^2-\left(\frac{7}{5}\right)^2{\small .}\)
Жауабы:\(\displaystyle 4{,}8{\small .}\)