Шеңберге сызылған тікбұрышты үшбұрыштың бір қабырғасы \(\displaystyle \sqrt{2}{\small . }\) Шектелген шеңбердің радиусы \(\displaystyle 1{\small . }\) Осы қабырғаға қарама-қарсы сүйір бұрышты табыңыз (жауабыңызды градуспен көрсетіңіз).
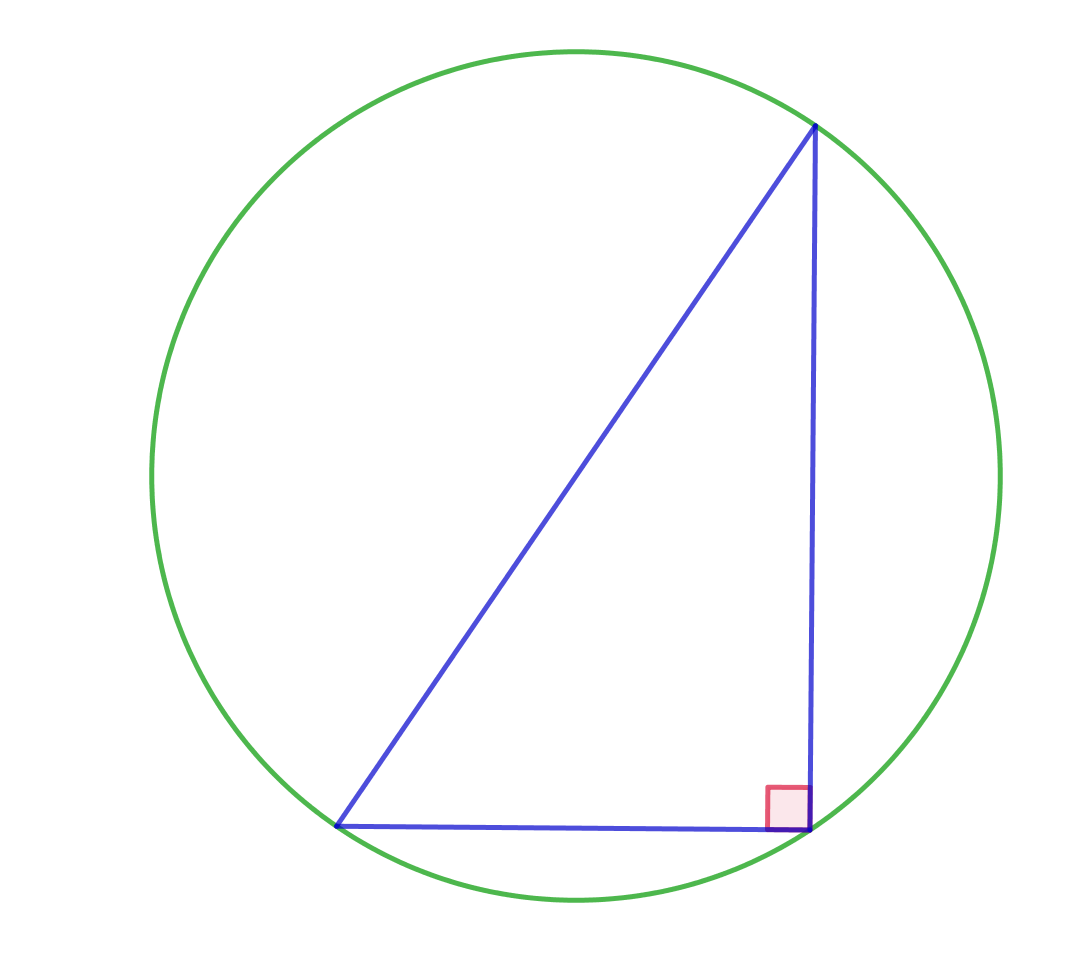
Шеңбер және тікбұрышты үшбұрыш
| Тік бұрышты үшбұрышты қоршап тұрған шеңбердің центрі гипотенузаның ортасында жатыр, ал оның радиусы гипотенузаның жартысына тең. | 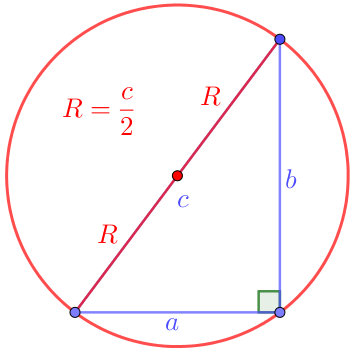 |
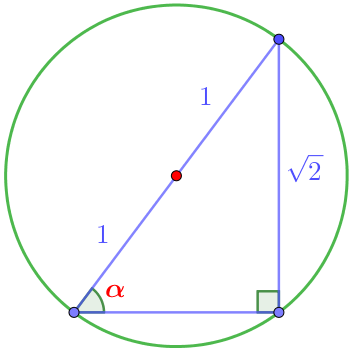 | Шеңбердің радиусы \(\displaystyle R=1{\small , }\) болғандықтан, тікбұрышты үшбұрыштың гипотенузасы \(\displaystyle c=2\cdot 1=2{\small }\) болады. Анықтау бойынша, тікбұрышты үшбұрыштағы бұрыштың синусы қарама-қарсы катеттің гипотенузаға қатынасына тең. Бұрыш \(\displaystyle \alpha \small\) ұзындық жағына \(\displaystyle \sqrt{2}\) қарама-қарсы жатсын. \(\displaystyle \sin\alpha=\frac{\sqrt{2}}{2}{\small .}\) |
Тікбұрышты үшбұрышта бұрыштар сүйір болғандықтан (тік бұрыштан басқа) және синустық мәндер кестесіне сәйкес , \(\displaystyle \sin45^{\circ}=\frac{\sqrt{2}}{2}{\small , }\) біз мынаны аламыз
\(\displaystyle \alpha=45^{\circ}{\small .}\)
Жауабы: \(\displaystyle 45{\small .}\)