\(\displaystyle ABCDEFGHIJ\) – дұрыс онбұрыш. Бұрышты табыңыз \(\displaystyle BCE{\small.}\) Жауабын градуспен беріңіз.
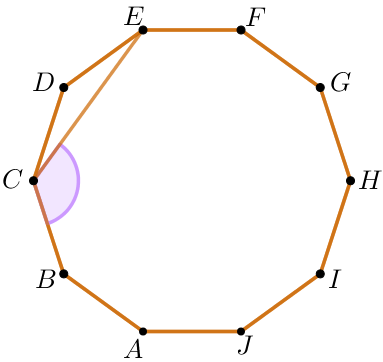
Дұрыс көпбұрыш-дөңес көпбұрыш, оның барлық қабырғалары мен іргелес қабырғалары арасындағы барлық бұрыштары тең..
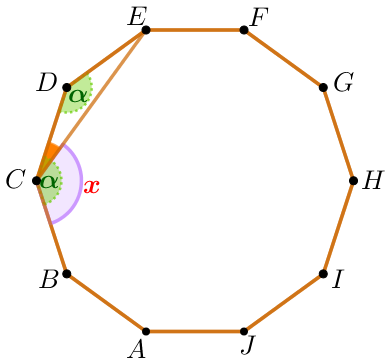 | Дұрыс онбұрыштың бұрышы тең болсын \(\displaystyle \color{darkgreen} \alpha \) және \(\displaystyle \angle BCE = \color{red}x {\small.}\) Тогда \(\displaystyle \color{red}x= \color{darkgreen} \alpha- \angle DCE{\small.}\)
\(\displaystyle \color{darkgreen} \alpha \) және \(\displaystyle \angle DCE{\small}\) бұрышты табамыз |
Формуланы пайдаланамыз.
Дұрыс көпбұрыштың төбесіндегі бұрыш \(\displaystyle \alpha_{n}=\frac{n-2}{n}\cdot 180^{\circ}{\small }\) тең, мұнда
\(\displaystyle n\) – дұрыс көпбұрыштың қабырғаларының саны.
Шарт бойынша \(\displaystyle n=10 {\small.}\) Аламыз \(\displaystyle \color{darkgreen} \alpha=\frac{n-2}{n}\cdot 180^{\circ}{\small ,} \\ \) \(\displaystyle \color{darkgreen} \alpha=\frac{10-2}{10}\cdot 180^{\circ}=\frac{8}{10}\cdot 180^{\circ}=144^{\circ}{\small .}\)
Демек, \(\displaystyle \angle BCD=\angle CDE=\color{darkgreen} \alpha =144^{\circ}{\small.}\) | 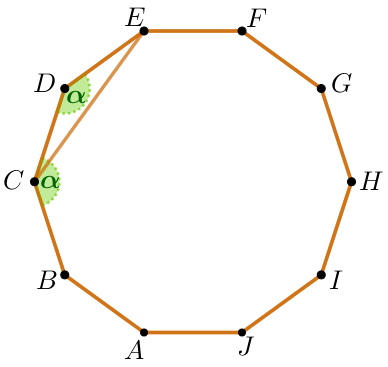 |
Үшбұрышты \(\displaystyle CDE {\small}\) қарастырайық
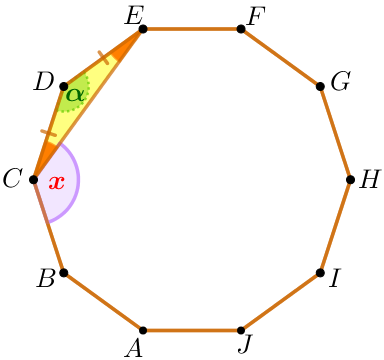 | Дұрыс көпбұрыштың қабырғалары тең болғандықтан, онда \(\displaystyle DC=DE {\small.}\) Демек, үшбұрыш \(\displaystyle CDE\) – теңбүйірлі. Теңбүйірлі үшбұрышта негіздегі бұрыштар тең болады. Үшбұрыштың ішкі бұрыштарының қосындысы \(\displaystyle 180^{\circ}{\small .} \) Онда \(\displaystyle \angle DCE= \angle DEC=\frac{180^{\circ}-\color{darkgreen} \alpha }{2} {\small ,} \\ \) \(\displaystyle \angle DCE= \frac{180^{\circ}-144^{\circ}}{2}=\frac{36^{\circ}}{2}=18^{\circ} {\small .} \) |
Аламыз
\(\displaystyle \color{red}x= \color{darkgreen} \alpha- \angle DCE=144^{\circ}-18^{\circ}=126^{\circ}{\small.}\)
Жауап: \(\displaystyle 126{\small.}\)