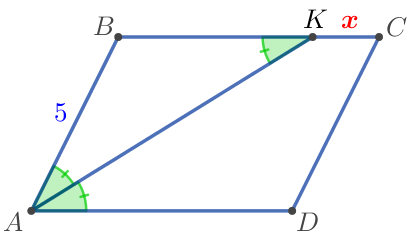
\(\displaystyle ABCD\) параллелограммасында \(\displaystyle K {\small}\) нүктесінде \(\displaystyle BC\) қиылысатын \(\displaystyle A {\small}\) бұрыштың биссектрисасы сызылған. егер \(\displaystyle AB=5 {\small}\) болса, ал параллелограмма периметрі \(\displaystyle 22 {\small} \) тең болса, \(\displaystyle KC {\small}\) табыңыз
Егер \(\displaystyle \color{red}x\) – \(\displaystyle KC {\small,}\) кесінді ұзындығы, онда \(\displaystyle \color{red}x=BC-BK {\small.}\) | 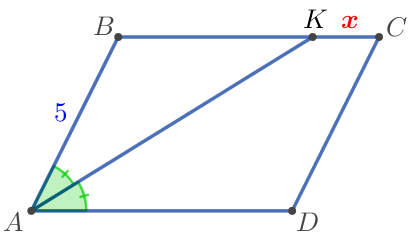 |
\(\displaystyle BC\) және \(\displaystyle BK {\small} \) кесінділерінің ұзындығын табыңыз.
Шарт бойынша \(\displaystyle ABCD\) параллелограмма периметрі \(\displaystyle 22 {\small,} \) тең \(\displaystyle AB=5 {\small.} \)
\(\displaystyle P_{ABCD}=2 \cdot (AB+BC) {\small,}\)
\(\displaystyle 22=2 \cdot (5+BC) {\small,}\)
\(\displaystyle 5+BC= 11{\small,}\)
\(\displaystyle BC=11-5=6 {\small.}\)
\(\displaystyle ABCD {\small:}\) параллелограммда
|
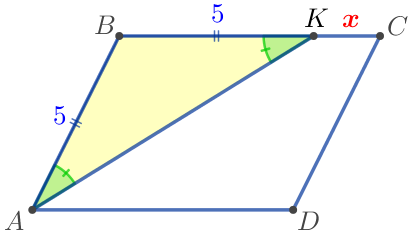
Шарт бойынша \(\displaystyle AK\) – биссектриса, демек \(\displaystyle \angle KAD= \angle KAB{\small.}\) Тиісінше, \(\displaystyle \angle KAB= \angle AKB{\small.}\) |
Үшбұрышты \(\displaystyle ABK {\small}\) қарастырайық
| Үшбұрышта \(\displaystyle ABK\) негіздегі бұрыштар тең болғандықтан, онда \(\displaystyle \triangle ABK\) – теңбүйірлі. Демек, \(\displaystyle BK=AB=5 {\small.}\) |
Аламыз
\(\displaystyle \color{red}x=BC-BK=6-5=1 {\small.}\)
Жауап: \(\displaystyle 1 {\small.}\)