Түзулер \(\displaystyle m\) және \(\displaystyle n\) параллель (суретті қараңыз). Егер \(\displaystyle \angle 1 =66^{\circ} {\small,}\) \(\displaystyle \angle 2=88^{\circ} {\small}\) болса, \(\displaystyle \angle 3 {\small}\) табыңыз. Жауабын градуспен беріңіз.

\(\displaystyle ^{\circ}\)
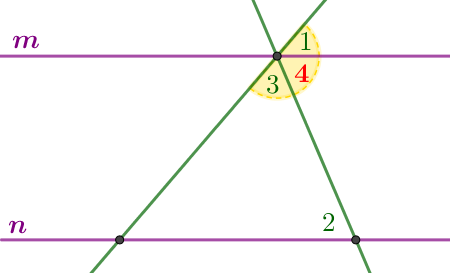 | Суреттегі бұрышты белгілеңіз \(\displaystyle {\color {red} 4} {\small.}\) Қосындыдағы \(\displaystyle 1 {\small,}\) \(\displaystyle 3\) және \(\displaystyle {\color {red} 4} \) бұрыштар кеңейтілген бұрышты құрайды. Сондықтан, \(\displaystyle \angle 1+ \angle {\color {red} 4}+\angle 3=180^{\circ} {\small.}\) |
Шарт бойынша түзу \(\displaystyle m\) және \(\displaystyle n\) параллель. \(\displaystyle \angle 2 \) және \(\displaystyle \angle {\color {red} 4}\) – көлденең жатқан бұрыштар. Сондықтан \(\displaystyle \angle {\color {red} 4}=\angle 2 {\small.}\) Онда \(\displaystyle \angle 1+\angle 2+ \angle 3=180^{\circ} {\small.}\) Аламыз \(\displaystyle 66^{\circ}+88^{\circ}+ \angle 3=180^{\circ} {\small,}\) \(\displaystyle \angle 3=180^{\circ}-(66^{\circ}+88^{\circ})=180^{\circ}-154^{\circ}=26^{\circ} {\small.}\) | 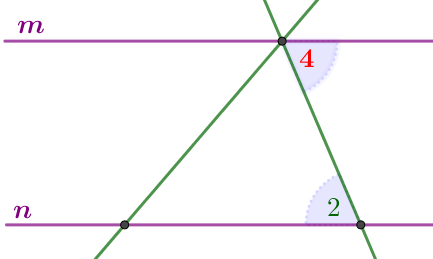 |
Жауап: \(\displaystyle 26{\small.}\)