От деревянного кубика отпилили все его вершины (см. рис.). Сколько граней у получившегося многогранника (невидимые рёбра на рисунке не изображены)?
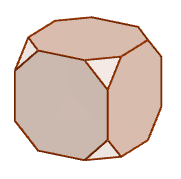
Подсчитаем количество граней и вершин куба до отпиливания.
Посмотрим, как изменится количество граней, если отпилить одну вершину так, как это показано на рисунке в условии.
Добавится ровно одна грань – грань сечения.
Тогда при отпиливании всех \(\displaystyle 8\) вершин количество граней увеличится на \(\displaystyle 8{\small.}\)
То есть:
\(\displaystyle \left.\begin{aligned}&\text{\small к 6 старым граням}\\&\text{\small добавятся 8 новых граней}\end{aligned}\right\} \text{\small всего 14 граней}\)
Итак, если отпилить у куба все вершины, то у получившегося многогранника будет \(\displaystyle 14\) граней.
Ответ: \(\displaystyle 14{\small.}\)