Кейбір түзу \(\displaystyle y=kx+b\,{\small}\) бейнеленген
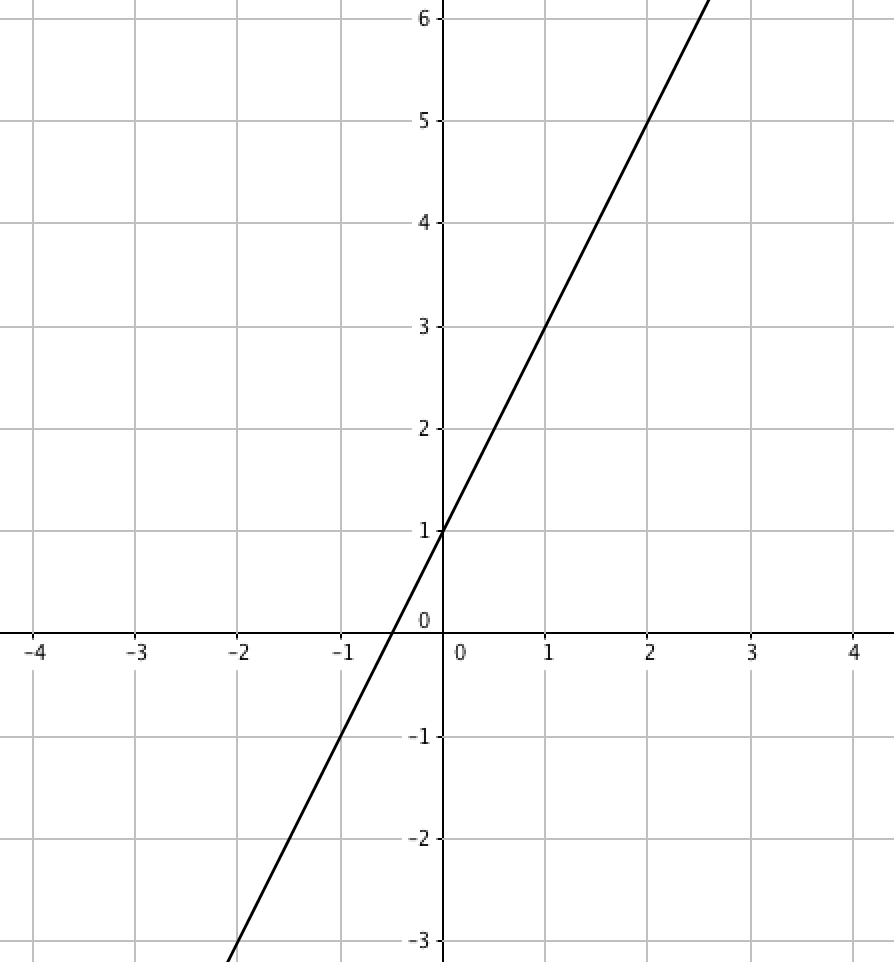
Нүктелердің координаттарын ауыстыру кезінде k және b коэффициенттері үшін теңдеулерді жазыңыз:
\(\displaystyle \left\{ \vphantom{\begin{aligned} 1\\[5px] 1 \end{aligned}} \right. \) | \(\displaystyle =k\,\cdot \)\(\displaystyle +b{\small ,}\) |
\(\displaystyle =k\,\cdot \)\(\displaystyle +b{\small .}\) |
Берілген түзуде біз екі ерікті A және B нүктені таңдаймыз .
Суреттегідей бүтін координаттары бар нүктелерді таңдау ыңғайлы:
Дұрыс жауап алу үшін берілген түзуде жатқан кез келген нүктелерді таңдауға болады.
A және B нүктелерінің координаттарын y = kx+b түзу теңдеуіне ауыстырайық, .
\(\displaystyle A(\color{blue}{ 1};\color{green}{3}) \) нүктеде \(\displaystyle x=\color{blue}{ 1}\) және \(\displaystyle y=\color{green}{ 3}{\small}\) координаттар бар, сондықтан
\(\displaystyle \color{green}{3}=k\cdot \color{blue}{ 1}+b \,{\small . }\)
\(\displaystyle B(\color{blue}{ 2};\color{green}{ 5}) \) нүктеде \(\displaystyle x=\color{blue}{ 2}\) және \(\displaystyle y=\color{green}{ 5}{\small}\) координаттар бар, сондықтан
\(\displaystyle \color{green}{ 5}=k\cdot \color{blue}{ 2}+b {\small . }\)
Осылайша, k және b коэффициенттерінің теңдеулері келесідей болады:
\(\displaystyle \left\{\begin{array}{rl}{\bf 3} &\kern{-1em}\,=k\cdot {\bf 1}+b {\small , }\\{\bf 5} &\kern{-1em}\,=k\cdot {\bf 2}+b {\small . }\end{array}\right.\)