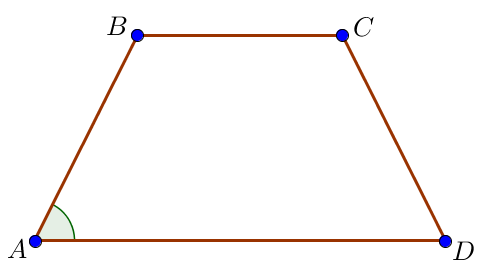
Тең қабырғалы трапецияның табандары \(\displaystyle 21\) және \(\displaystyle 5\small,\) биіктігі \(\displaystyle 8\small.\) Трапецияның сүйір бұрышын табыңыз. Жауабыңызды градуспен беріңіз.
\(\displaystyle AD=21\) және \(\displaystyle BC=5\) – табандары, \(\displaystyle AB=CD\) – қабырғалары, \(\displaystyle BH=CK=8 \) – тең қабырғалы трапецияның \(\displaystyle ABCD\small\) биіктіктері болсын Трапецияның табандары параллель және трапецияның биіктіктері табандарына перпендикуляр болғандықтан \(\displaystyle BH K C \) – тік төртбұрыш. Сонда \(\displaystyle H K =BC=5 \small.\) | 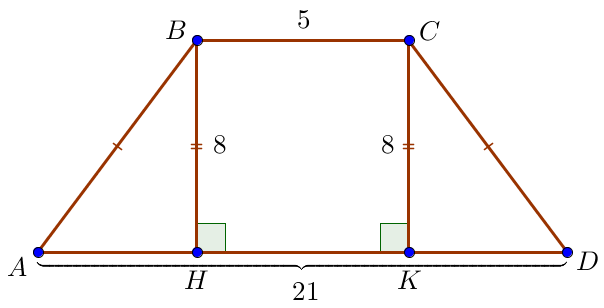 |
Тікбұрышты үшбұрыштар \(\displaystyle ABH\) және \(\displaystyle DCK\) гипотенузада \(\displaystyle AB=CD\) және катетінде \(\displaystyle BH=CK\small\) тең. Демек, \(\displaystyle AH=DK\) және \(\displaystyle AH=DK=\frac{AD-BC}{2}\small,\) \(\displaystyle AH=\frac{21-5}{2}=\frac{16}{2}=8\small.\) | 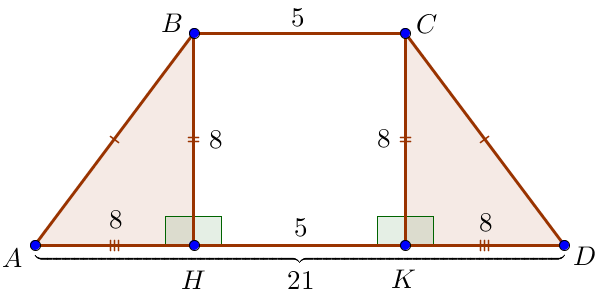 |
Үшбұрыштан трапецияның \(\displaystyle CKD\small\) сүйір бұрышын табамыз Өйткені \(\displaystyle CK=KD=8\small,\) онда үшбұрыш \(\displaystyle CKD\) – тең қабырғалы болады. Сонда тең қабырғалы үшбұрыштың қасиеті бойынша, \(\displaystyle \angle KCD=\angle KDC\small.\) Үшбұрыштың бұрыштарының қосындысы \(\displaystyle 180^{\circ}\small,\) сондықтан \(\displaystyle \angle KCD=\frac{1}{2}(180^{\circ}-\angle CKD )\small,\) \(\displaystyle \angle KCD=\frac{1}{2}(180^{\circ}-90^{\circ})=\frac{1}{2}\cdot 90^{\circ}=45^{\circ}\small.\) | 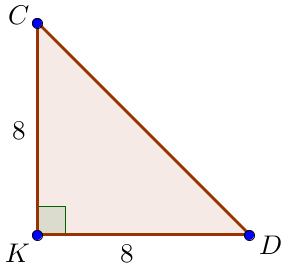 |
Жауабы: \(\displaystyle 45 \small.\)