Skip to main content

Теориясы: Бұрыштар

Тапсырма

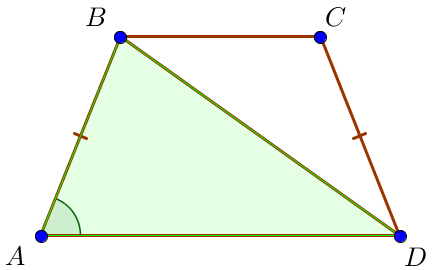
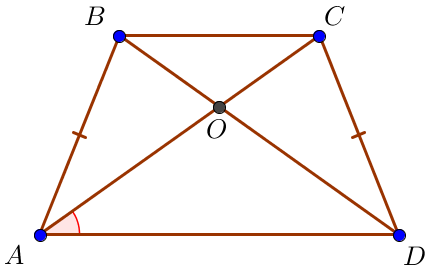
Негіздері \(\displaystyle AD\) және \(\displaystyle BC\)  болатын, \(\displaystyle ABCD\) тең қабырғалы трапецияда \(\displaystyle O\) - диагональдардың қиылысу нүктесі, \(\displaystyle CAD\) бұрышы \(\displaystyle 36^\circ \small\)- ге тең.Бұрыш \(\displaystyle AOD\ \small\) неге тең? Жауабын градуспен көрсетіңіз.

Шешім

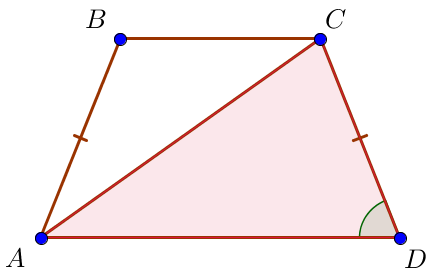
 \(\displaystyle ABD\) және \(\displaystyle ACD\small\) үшбұрыштарын қарастырайық

Олар екі жағында және олардың арасындағы бұрышта тең:

  • \(\displaystyle AB=CD\) тең қабырғалы трапецияның қабырғалары ретінде,
  • \(\displaystyle \angle BAD= \angle CDA\) тең қабырғалы трапеция табанындағы бұрыштар ретінде,
  • \(\displaystyle AD\) – ортақ жағы.

Сонымен \(\displaystyle ADB\) және \(\displaystyle DAC\) бұрыштары тең.

 

Содан кейін

\(\displaystyle \angle ADB=\angle CAD=36^{\circ}\small.\)

 

Үшбұрыштан  \(\displaystyle AOD\)

\(\displaystyle \angle AOD=180^{\circ} - \angle OAD - \angle ODA=\)

\(\displaystyle =180^{\circ} - 36^{\circ} - 36^{\circ} = 108^{\circ}\small. \)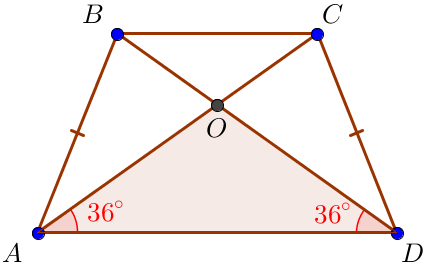

Жауабы: \(\displaystyle 108^{\circ}{\small .}\)