В равнобедренной трапеции \(\displaystyle ABCD\) на основании \(\displaystyle AD\) выбрали точку \(\displaystyle K\) так, что прямая \(\displaystyle CK\) параллельна \(\displaystyle AB\small,\) угол \(\displaystyle KCD\) равен \(\displaystyle 28^\circ\small.\) Чему равен угол \(\displaystyle A\ \small?\) Ответ дайте в градусах.
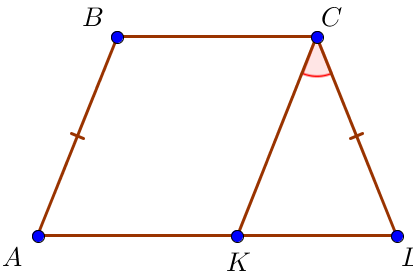
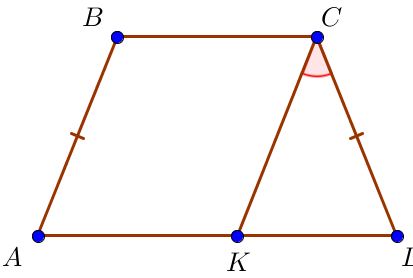
При пересечении параллельных прямых \(\displaystyle AB\) и \(\displaystyle CK\) секущей \(\displaystyle AD\) соответственные углы равны, значит
\(\displaystyle \angle CKD=\angle BAD\small.\)
В четырехугольнике \(\displaystyle ABCK\) противоположные стороны параллельны, поэтому \(\displaystyle ABCK\) – параллелограмм.
Тогда \(\displaystyle CK=AB\) как противоположные стороны параллелограмма.
Рассмотрим треугольник \(\displaystyle CKD.\) Так как \(\displaystyle CK=AB=CD\small,\\\) то \(\displaystyle \triangle CKD\) – равнобедренный. По свойству равнобедренного треугольника \(\displaystyle \angle CDK=\angle CKD\small.\) Следовательно, \(\displaystyle \angle CKD=\frac{180^{\circ} - \angle KCD}{2}=\) \(\displaystyle =\frac{180^{\circ} - 28^{\circ}}{2}= \frac{152}{2}=76^{\circ}\small. \) | 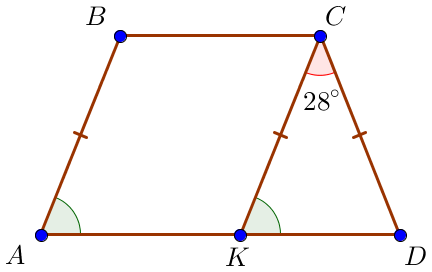 |
Получаем
\(\displaystyle \angle A=\angle CKD=76^{\circ}\small. \)
Ответ: \(\displaystyle 76^\circ \small.\)