Тең бүйірлі \(\displaystyle ABCD\) трапецияда \(\displaystyle AD\) табаныңда \(\displaystyle K\) нүктесі таңдалды, сонда \(\displaystyle CK\) түзуі \(\displaystyle АВ\)- ға параллель , \(\displaystyle KCD\) бұрышы \(\displaystyle 28^\circ\small\) -қа тең. \(\displaystyle A\ \small\) бұрышы неге тең? Жауабын градуспен көрсетіңіз .
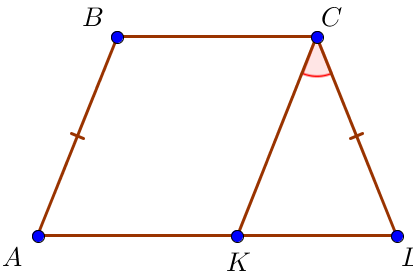
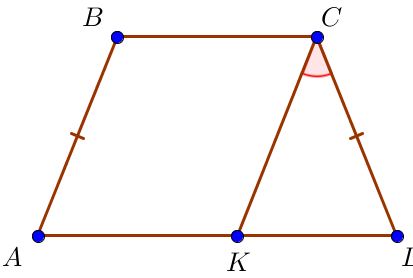
Параллель түзулердің \(\displaystyle AB\) және \(\displaystyle CK\) қимасының \(\displaystyle AD\) қиылысында сәйкес бұрыштар тең болады, яғни
\(\displaystyle \angle CKD=\angle BAD\small.\)
\(\displaystyle ABCK\) төртбұрышта қарама-қарсы қабырғалар параллель, сондықтан \(\displaystyle ABCK\) – параллелограмм болады.
Сонда \(\displaystyle CK=AB\) параллелограмның қарама-қарсы қабырғалары ретінде.
\(\displaystyle CKD\small\) үшбұрышын қарастырайық \(\displaystyle CK=AB=CD\small\\\) болғандықтан \(\displaystyle \triangle CKD\) – тең қабырғалы болады. Тең қабырғалы үшбұрыштың қасиеті бойынша \(\displaystyle \angle CDK=\angle CKD\small.\) Демек, \(\displaystyle \angle CKD=\frac{180^{\circ} - \angle KCD}{2}=\) \(\displaystyle =\frac{180^{\circ} - 28^{\circ}}{2}= \frac{152}{2}=76^{\circ}\small. \) | 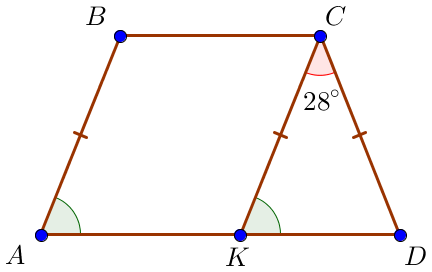 |
Біз алып жатырмыз
\(\displaystyle \angle A=\angle CKD=76^{\circ}\small. \)
Жауабы: \(\displaystyle 76^\circ \small.\)