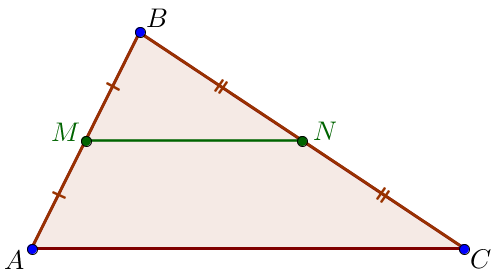
Үшбұрышта \(\displaystyle АВС\) сәйкесінше \(\displaystyle ВС\) және \(\displaystyle АС\) қабырғаларының ортаңғы нүктелері \(\displaystyle M\) және \(\displaystyle N\) белгіленген. Төртбұрыштың ауданы \(\displaystyle ABMN\) \(\displaystyle 171{\small.}\) Үшбұрыштың \(\displaystyle CNM{\small}\) ауданын табыңыз
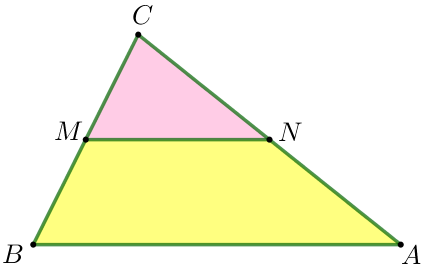 | Төртбұрыштың ауданы \(\displaystyle ABMN \) үшбұрыштардың аудандары \(\displaystyle ABC\) және \(\displaystyle CNM {\small}\) арасындағы айырмашылыққа тең \(\displaystyle S_{ABMN}=S_{\triangle ABC}-S_{\triangle CNM} {\small.}\)
|
Үшбұрыштарды \(\displaystyle CNM\) және \(\displaystyle ABC {\small} \\ \) қарастырайық
\(\displaystyle M\) және \(\displaystyle N\) – нүктелері сәйкесінше \(\displaystyle BC\) және \(\displaystyle AC\) қабырғаларының ортаңғы нүктелері болғандықтан, \(\displaystyle MN\) – үшбұрыштың \(\displaystyle ABC {\small}\) орта сызығы
\(\displaystyle MN \parallel AB\) және \(\displaystyle MN=\frac{1}{2}\cdot AB\small. \)
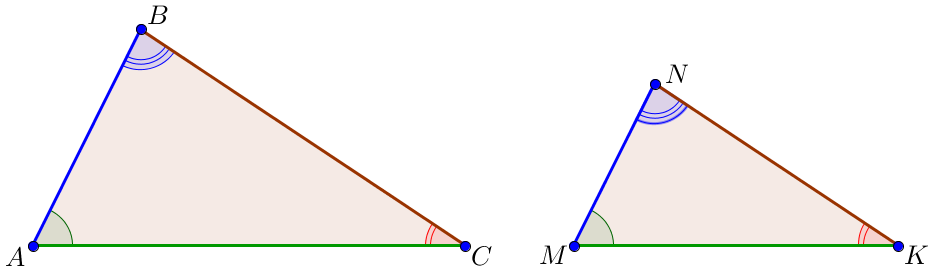
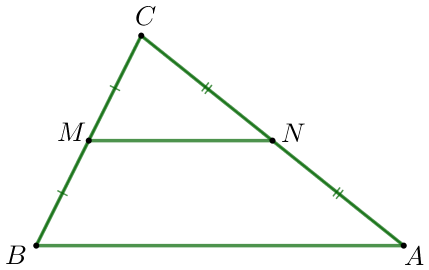 | Үшбұрыштарда \(\displaystyle CNM\) және \(\displaystyle ABC \) аламыз:
\(\displaystyle \frac{CM}{BC}= \frac{CN}{AC}=\frac{MN}{AB}=\frac{1}{2}\small. \) |
Ұқсас үшбұрыштарда ұқсастық коэффициенті \(\displaystyle k\) ұқсас қабырғалардың қатынасына тең. білдіреді,
\(\displaystyle k=\frac{MN}{AB}=\frac{1}{2} {\small.} \)
\(\displaystyle \frac{S_{\triangle CNM}}{S_{\triangle ABC}}=k^2 {\small,} \\ \)
\(\displaystyle S_{\triangle ABC}=\frac{{S_{\triangle CNM}}}{k^2}{\small,} \\ \)
\(\displaystyle S_{\triangle ABC}=\frac{S_{\triangle CNM}}{{\big(\frac{1}{2}\big)}^2}=\frac{S_{\triangle CNM}}{\frac{1}{4}}=4\cdot S_{\triangle CNM}{\small.} \\ \)
Біз алып жатырмыз
\(\displaystyle S_{ABMN}=S_{\triangle ABC}-S_{\triangle CNM} =4\cdot S_{\triangle CNM}- S_{\triangle CNM}=3\cdot S_{\triangle CNM}{\small.}\\ \)
Демек,
\(\displaystyle S_{\triangle CNM}=\frac{1}{3}\cdot S_{ABMN}=\frac{1}{3}\cdot 171=57{\small.}\)
Жауабы: \(\displaystyle 57 {\small.}\)