Точка \(\displaystyle H\) является основанием высоты, проведённой из вершины прямого угла \(\displaystyle B\) треугольника \(\displaystyle ABC\) к гипотенузе \(\displaystyle AC {\small.}\) Найдите \(\displaystyle BC {\small,}\) если \(\displaystyle AH=18 {\small,}\) \(\displaystyle AC=50 {\small.}\)
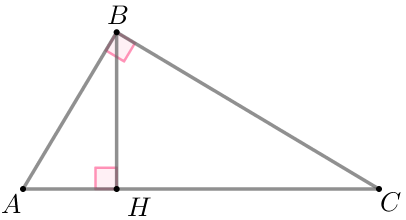
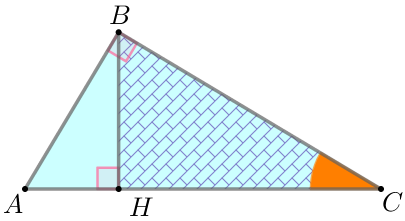 | Прямоугольные треугольники \(\displaystyle ABC\) и \(\displaystyle BHC\) подобны по острому углу. Следовательно, \(\displaystyle \frac{BC}{AC}=\frac{CH}{BC} {\small,}\\ \) \(\displaystyle BC^2=CH \cdot AC {\small.}\) |
По условию \(\displaystyle AC=50 {\small,}\) \(\displaystyle AH=18 {\small,}\) тогда
\(\displaystyle CH=AC-AH=50-18=32{\small.}\)
Получаем
\(\displaystyle BC^2=CH \cdot AC =32 \cdot 50=1600 =40^2{\small.}\)
Так как длина отрезка не может быть отрицательной, то \(\displaystyle BC=40{\small.}\)
Ответ: \(\displaystyle 40 {\small.}\)