\(\displaystyle Н\) нүктесі үшбұрыштың \(\displaystyle АВС\) тік бұрыш төбесінен \(\displaystyle В\) гипотенузаға \(\displaystyle АС \) түсірілген биіктіктің табаны болып табылады. Егер \(\displaystyle AH=18 {\small,}\) \(\displaystyle AC=50 {\small}\) болса \(\displaystyle BC {\small}\) табыңыз.
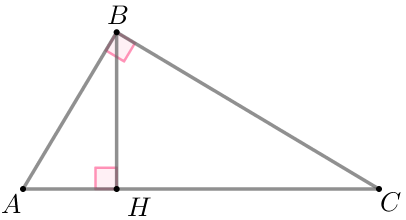
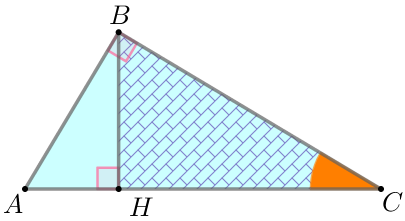 | Тік бұрышты үшбұрыштар \(\displaystyle ABC\) және \(\displaystyle BHC\) сүйір бұрыштары бойынша ұқсас. Демек, \(\displaystyle \frac{BC}{AC}=\frac{CH}{BC} {\small,}\\ \) \(\displaystyle BC^2=CH \cdot AC {\small.}\) |
Шарты бойынша \(\displaystyle AC=50 {\small,}\) \(\displaystyle AH=18 {\small,}\) онда
\(\displaystyle CH=AC-AH=50-18=32{\small.}\)
Біз алып жатырмыз
\(\displaystyle BC^2=CH \cdot AC =32 \cdot 50=1600 =40^2{\small.}\)
Кесіндінің ұзындығы теріс болуы мүмкін емес болғандықтан \(\displaystyle BC=40{\small.}\)
Жауабы: \(\displaystyle 40 {\small.}\)