Теориясы: Ауданы.

Есептің шарты бойынша сызбаны орындаймыз.

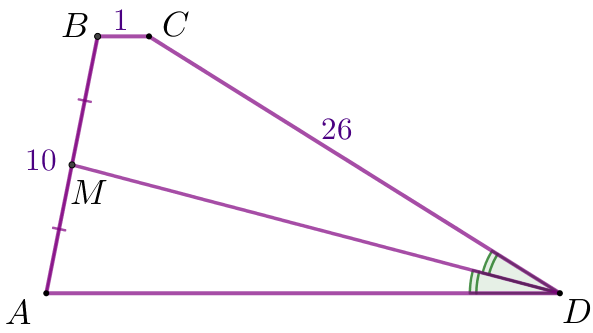\(\displaystyle ABCD\) – трапеция, онда: \(\displaystyle AD\) және \(\displaystyle BC=1\) – табандар; \(\displaystyle AB=10\) және \(\displaystyle CD=26\) – бүйір қабырғалар; \(\displaystyle M\) –  \(\displaystyle AB{\small}\) қабырғасының ортасы \(\displaystyle DM\) –  \(\displaystyle ADC {\small}\) бұрышының биссектрисасы

 \(\displaystyle ABCD {\small}\) трапециясының биіктігін табу қажет

 \(\displaystyle ABCD {\small}\) трапециясының \(\displaystyle AD\) табанын табайық

Әрі қарай, трапецияның барлық қабырғаларының ұзындығын біле отырып, трапецияның биіктігінің ұзындығын есептей аламыз.

Табан ұзындықтарының жарты қосындысы трапецияның ортаңғы сызығының ұзындығына тең екенін ескереміз.

Қосымша сызбаны орындайық. 

\(\displaystyle MN\) –  \(\displaystyle ABCD {\small}\) трапециясының ортаңғы сызығы болсын Сонда

\(\displaystyle MN=\frac{AD+BC}{2} {\small;}\\ \) \(\displaystyle MN \parallel BC\) және \(\displaystyle MN \parallel AD {\small;}\\ \) \(\displaystyle N\) – нүктесі \(\displaystyle CD\) бүйір қабырғасының ортасы және \(\displaystyle \\ CN=ND=\frac{1}{2} \cdot CD=\frac{1}{2} \cdot 26=13 {\small.}\)

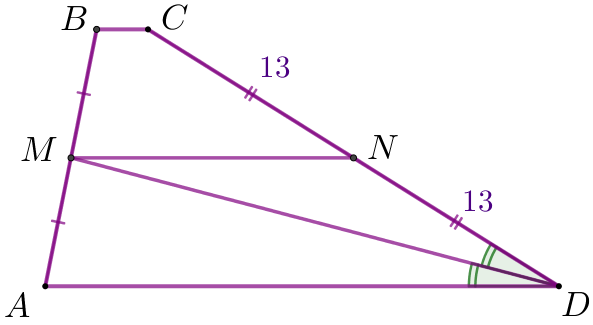\(\displaystyle MN \parallel AD\) және \(\displaystyle DM\) – қима болғандықтан, онда \(\displaystyle \angle ADM= \angle DMN\) (көлденең жатқан бұрыштар). Шарт бойынша   \(\displaystyle DM\) –  \(\displaystyle ADC {\small,}\) бұрышының биссектрисасы, демек \(\displaystyle \angle ADM= \angle MDN {\small.}\)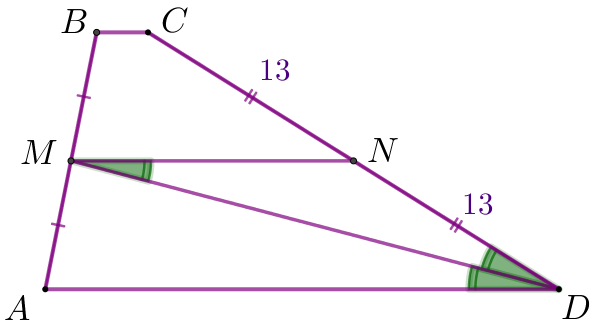

Төмендегіні аламыз

\(\displaystyle \angle DMN= \angle MDN {\small.}\)

 \(\displaystyle DMN {\small}\) үшбұрышын қарастырайық 

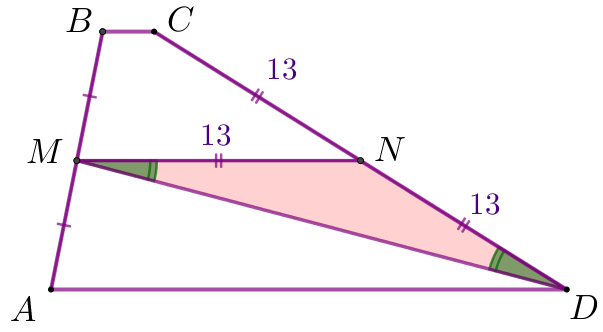\(\displaystyle DMN \) үшбұрышының \(\displaystyle DM \) қабырғасындағы бұрыштар тең. Демек ,   \(\displaystyle \triangle DNM \) – теңбүйірлі. Демек, \(\displaystyle MN=ND=13 {\small.}\)

Төмендегіні аламыз

\(\displaystyle MN=\frac{AD+BC}{2} {\small;}\)

\(\displaystyle 13=\frac{AD+1}{2} {\small;}\)

\(\displaystyle 26=AD+1 {\small;}\)

\(\displaystyle AD=25 {\small.}\)

\(\displaystyle ABCD {\small}\) трапециясының  \(\displaystyle BH\) биіктігін табайық

Қосымша сызбаларды орындайық:

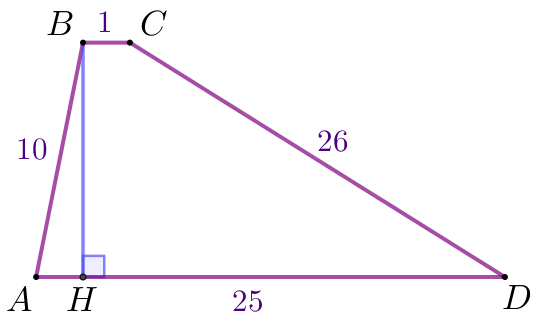
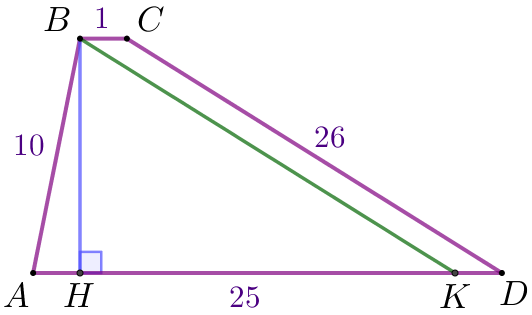
\(\displaystyle 1{\small}\)  \(\displaystyle B\) нүктесінен \(\displaystyle BH{\small}\) биіктігін түсірейік		\(\displaystyle 2{\small}\)  \(\displaystyle CD{\small}\) қабырғасына параллель \(\displaystyle BK\) кесіндісін салайық

Сурет бойынша \(\displaystyle BH\) –  \(\displaystyle ABCD\) трапециясының биіктігі және \(\displaystyle ABK {\small}\) үшбұрышының биіктігі екенін байқаймыз

 \(\displaystyle ABK {\small}\) үшбұрышының қабырғаларының ұзындығын табыңыз. Содан кейін үшбұрыштың қабырғаларының ұзындығын біле отырып, оның биіктігін есептей аламыз.

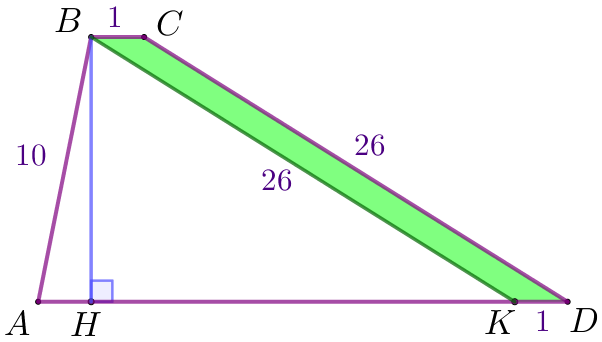\(\displaystyle BCDK\) төртбұрышында жақтары жұптасып параллель болады. Демек, \(\displaystyle BCDK\) – параллелограмм. Параллелограммда қарама-қарсы қабырғалар жұптасып тең болады. Яғни \(\displaystyle KD=BC=1 \)  және \(\displaystyle BK=CD=26 {\small.}\)

  \(\displaystyle AK\) кесіндісінің ұзындығы \(\displaystyle AD\) және \(\displaystyle KD {\small}\) кесінділерінің ұзындығының айырмасына тең

\(\displaystyle AK=AD-KD=25-1=24 {\small.}\)

 \(\displaystyle ABK {\small}\) үшбұрышын қарастырайық 

\(\displaystyle AB=10 {\small;}\) \(\displaystyle AK=24{\small;}\)\(\displaystyle BK=26{\small.}\)   \(\displaystyle 10^2+24^2=100+576=676=26^2 {\small}\) ескерейік Яғни \(\displaystyle AB^2+AK^2=BK^2 {\small.}\)

\(\displaystyle ABK\) – үшбұрышы– тікбұрышты, бұл ретте \(\displaystyle BK\) – гипотенуза, \(\displaystyle AB\) және \(\displaystyle AK\) – катеттер. Яғни

\(\displaystyle AB \perp AK{\small.}\)

Демек , \(\displaystyle BA\) – бұл  \(\displaystyle ABK {\small}\) үшбұрышының биіктігі Демек,

\(\displaystyle BH=BA=10 {\small.}\)

Жауабы: \(\displaystyle 10 {\small.}\)