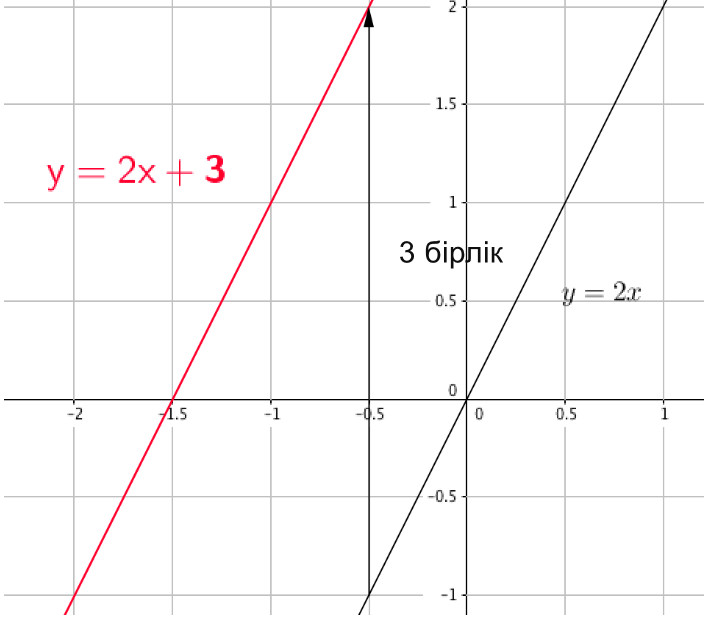
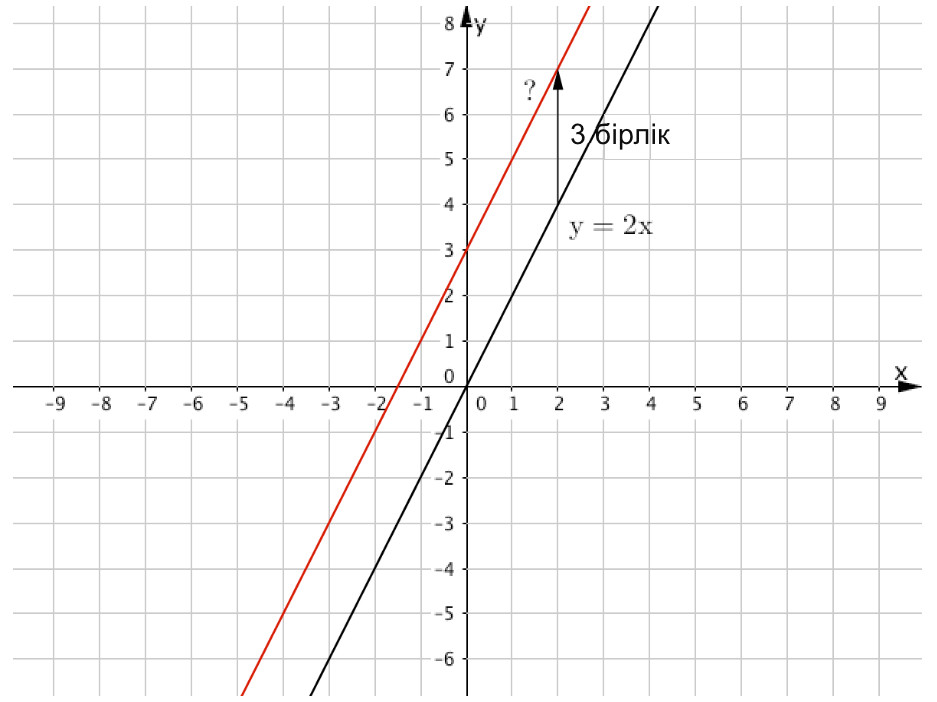
\(\displaystyle y=2x\) түзуін \(\displaystyle 3\)бірлікке жоғары жылжыту арқылы алынған түзудің теңдеуін жазыңыз (\(\displaystyle \rm OY\) осі бойымен).
\(\displaystyle y=2x\)
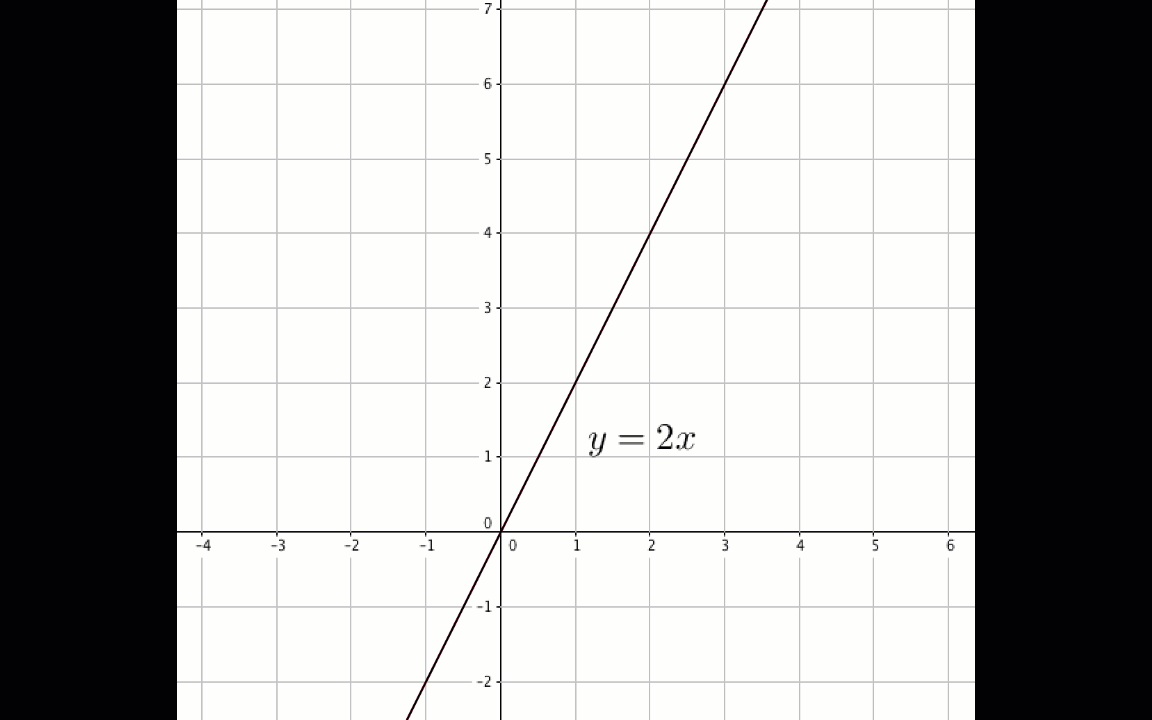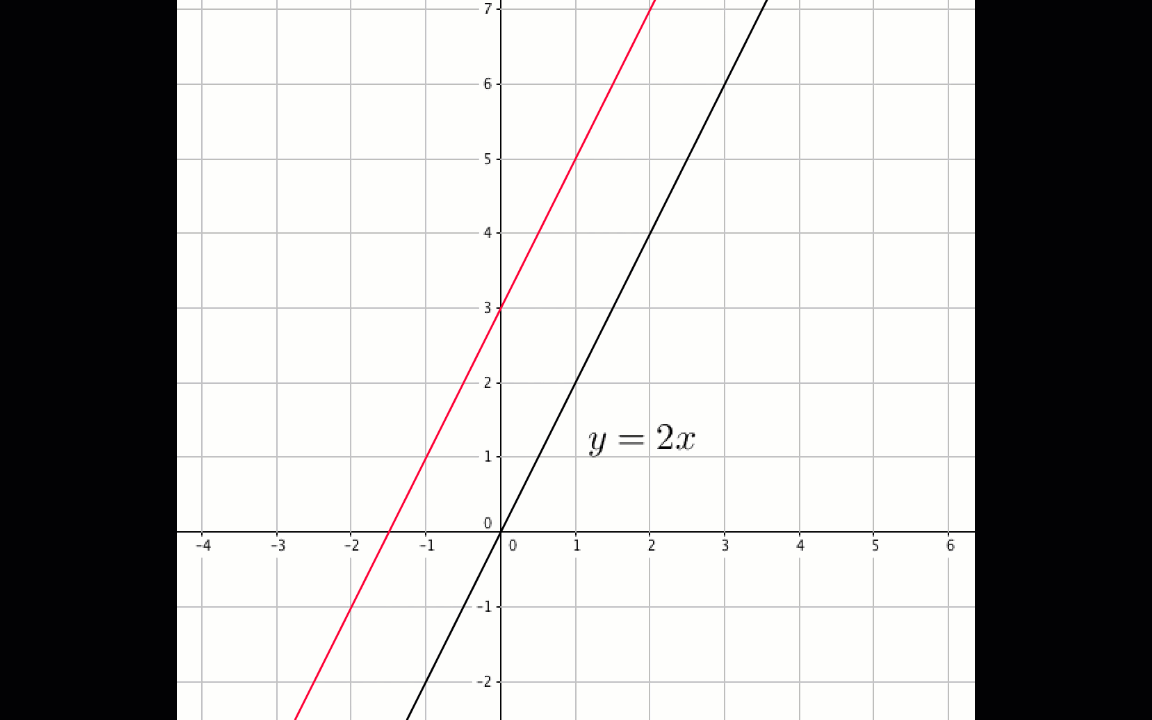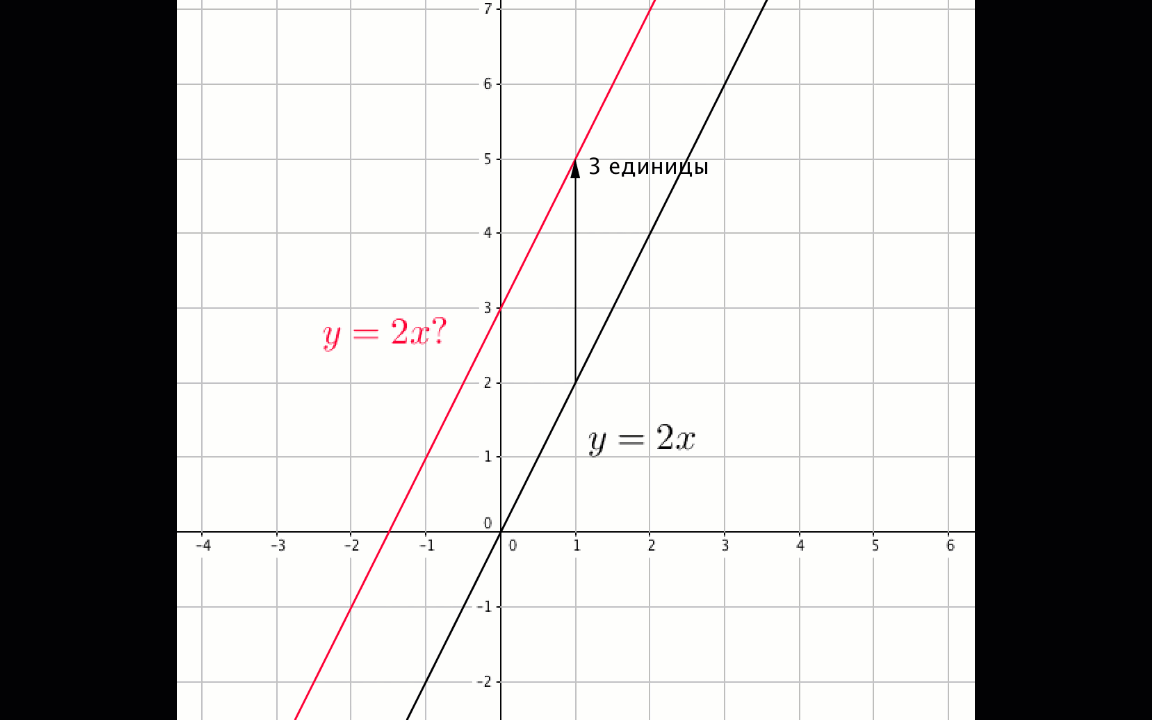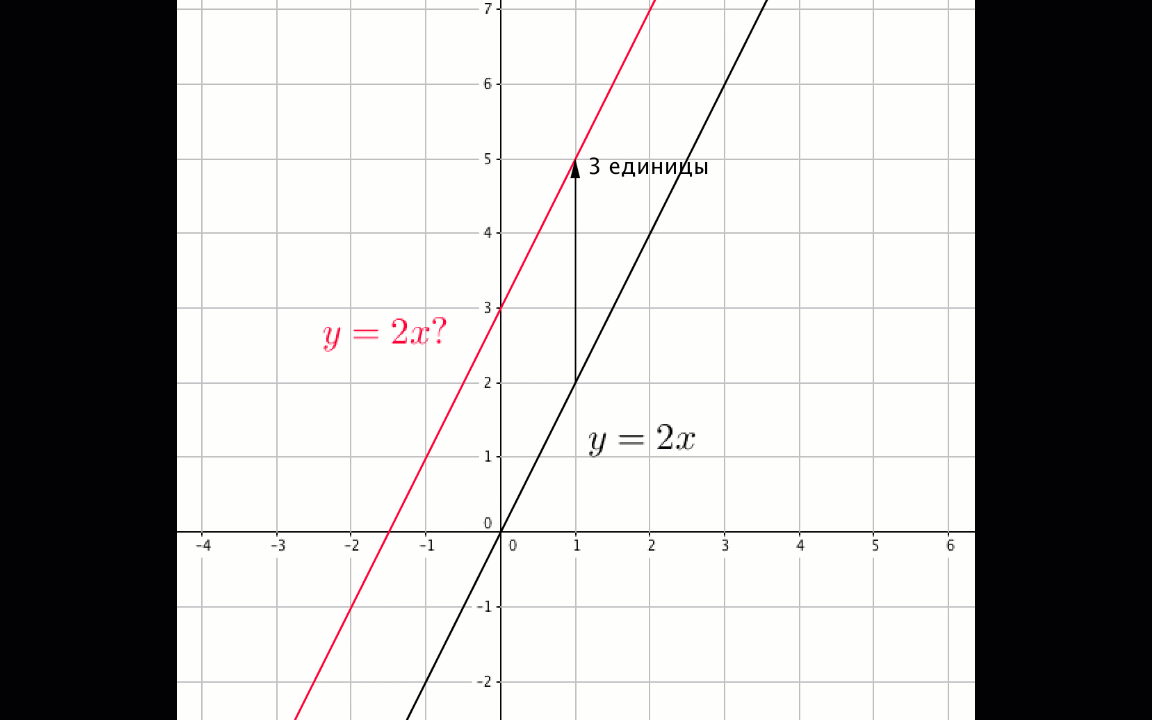
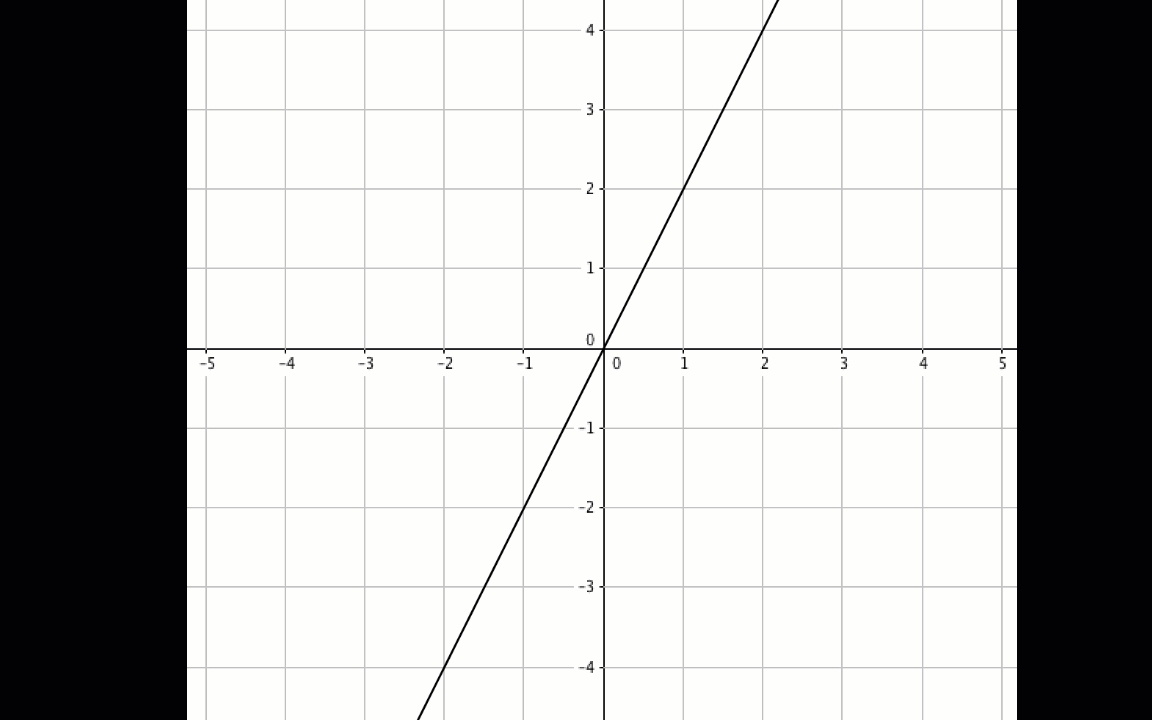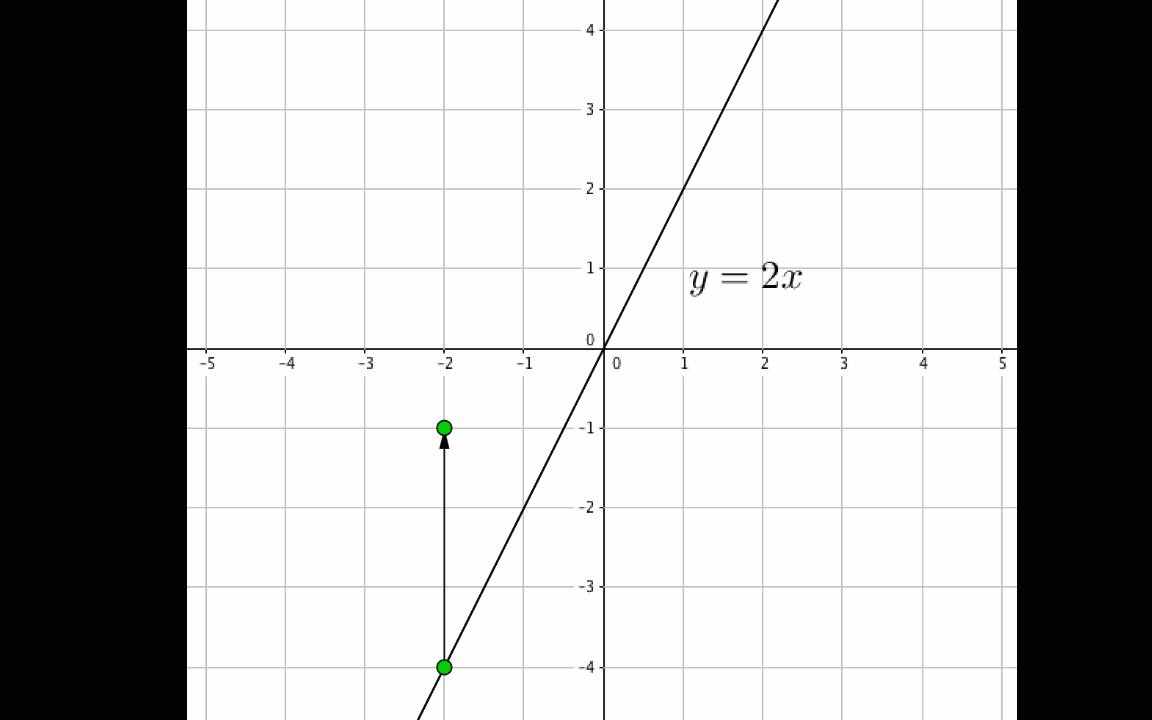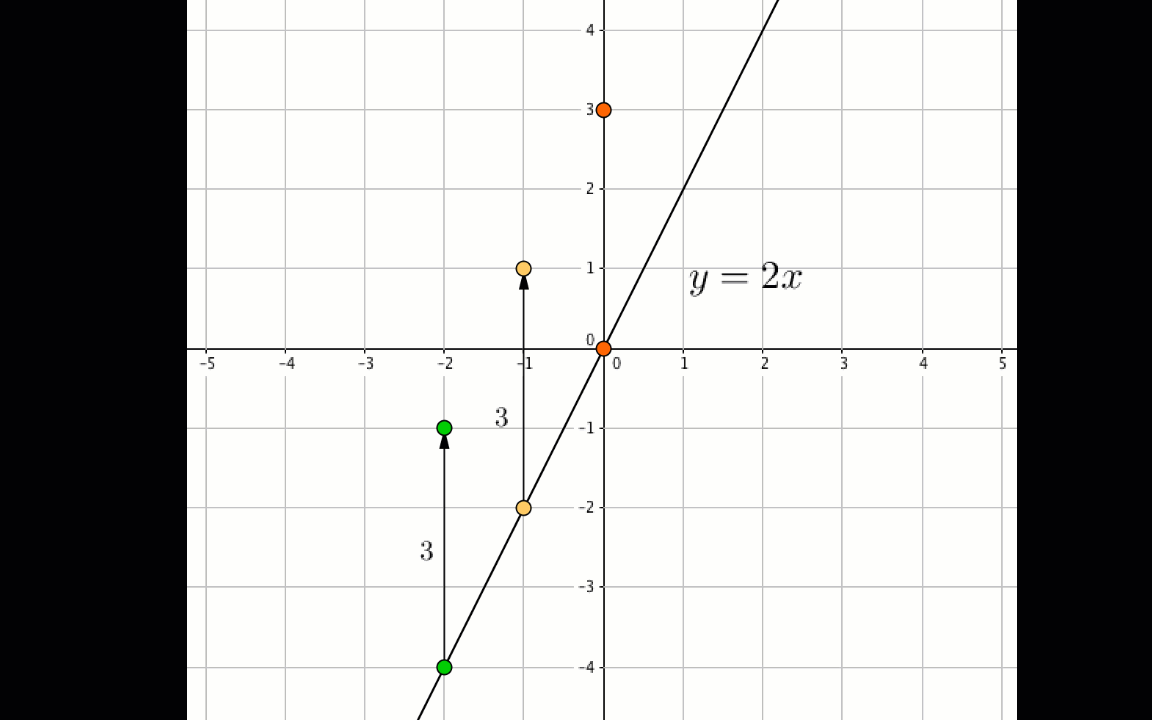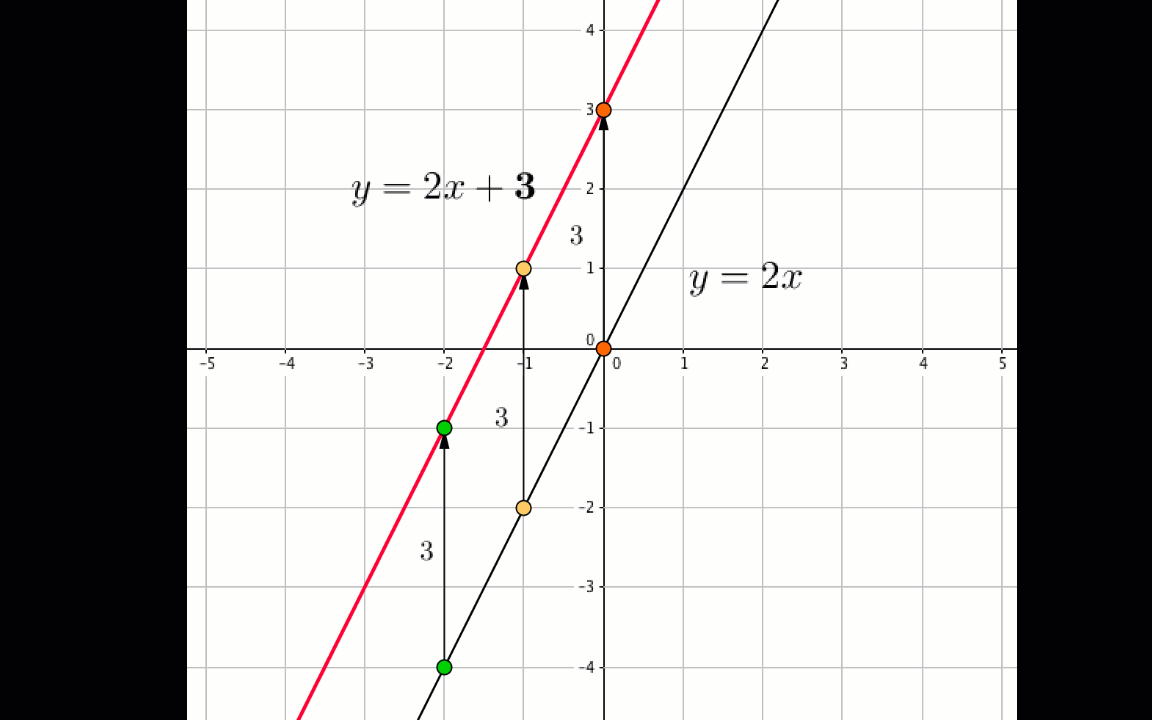
Егер координаттары \(\displaystyle (x\,; y\,)\) кейбір нүктелерді \(\displaystyle \rm A\) бірліктеріне жоғары көтерсе, онда координаттары \(\displaystyle (x\,; y+{\rm A}\,){\small }\) нүктені аламыз :

Сондықтан біз ережені келесідей тұжырымдай аламыз.
Егер \(\displaystyle y=f(x\,) \) функциясының графигін \(\displaystyle \color{blue}{\rm A} \) бірліктеріне жоғары көтерсеңіз, онда \(\displaystyle y=f(x\,)+\color{blue}{\rm A}{\small } \) функциясының графигі алынады .
Бізге \(\displaystyle y=3x{\small } \) функциясының графигі берілген . Біз оны \(\displaystyle \color{blue}{ 3}\) бірлікке жоғары көтереміз.
Сонда ережеге сәйкес бізде келесідей функция графигі болады:
\(\displaystyle y= 2x+\color{blue}{ 3}{\small . }\)