Суретте төрт түзу көрсетілген: \(\displaystyle a{\small ,}\) \(\displaystyle b{\small ,}\) \(\displaystyle c\) және \(\displaystyle d{\small .}\) Қайсысы сызықтық функцияның графигі \(\displaystyle y=-2x+6{\small ? }\)
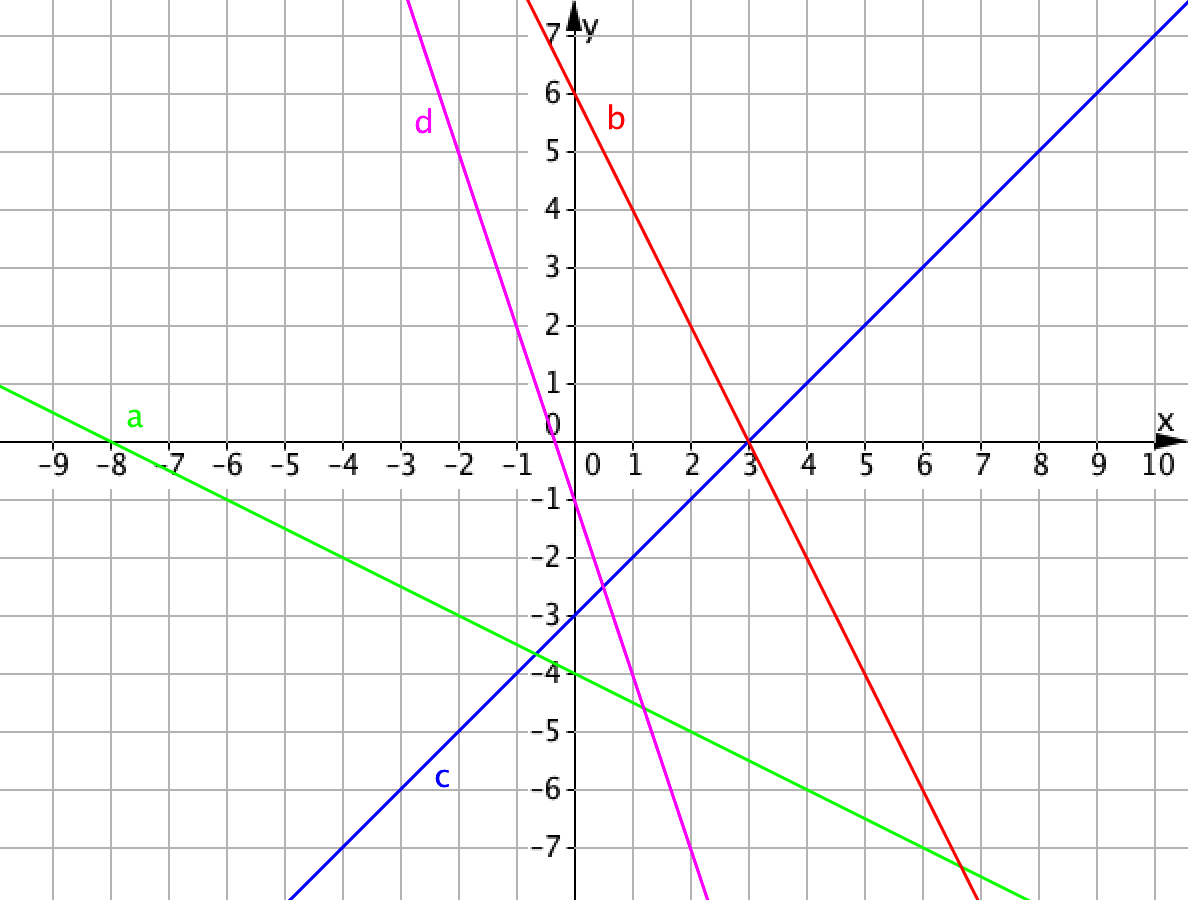
Егер түзу \(\displaystyle y=-2x+6\) сызықтық функциясының графигі болса және белгілі бір нүктеден өтсе, онда бұл нүкте \(\displaystyle y=-2x+6{\small . }\)теңдеуін қанағаттандыратынын еске салайық.
Түзулер өтетін кез келген нүктелерді ретімен аламыз және бұл нүктелер \(\displaystyle y=-2x+6{\small }\)теңдеуіне сәйкес келетіндігін тексереміз:
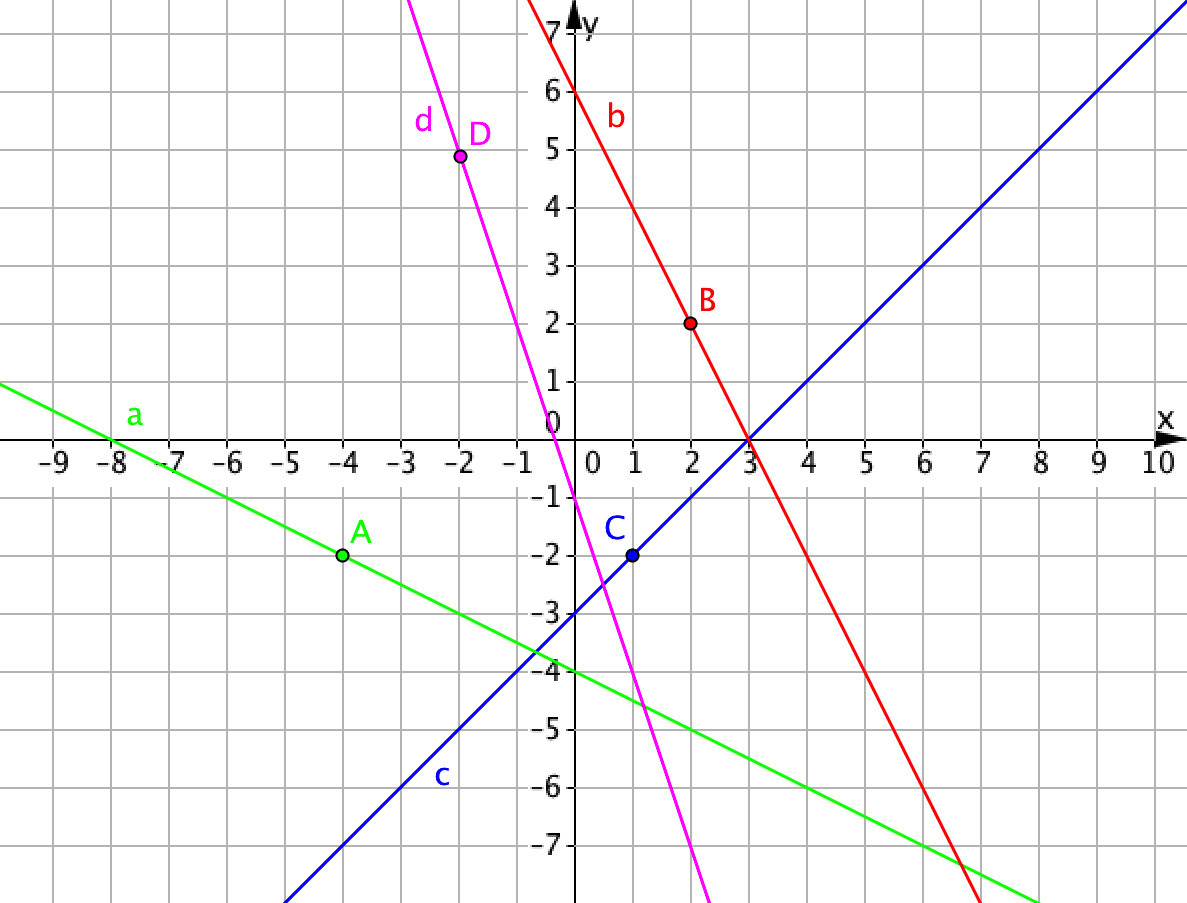
| Түзу | Түзу нүктесі | \(\displaystyle y=-2x+6\)функциясы | Нәтиже |
| \(\displaystyle a \) | \(\displaystyle (\color{blue}{-4};\color{green}{-2}) \) | \(\displaystyle \color{green}{-2}=-2\cdot (\color{blue}{-4})+6;\) \(\displaystyle -2=14\) | қате |
| \(\displaystyle b \) | \(\displaystyle (\color{blue}{2};\color{green}{2}) \) | \(\displaystyle \color{green}{2}=-2\cdot \color{blue}{2}+6;\) \(\displaystyle 2=2\) | дұрыс |
| \(\displaystyle c \) | \(\displaystyle (\color{blue}{1};\color{green}{-2}) \) | \(\displaystyle \color{green}{-2}=-2\cdot \color{blue}{1}+6\) \(\displaystyle -2=4\) | қате |
| \(\displaystyle d \) | \(\displaystyle (\color{blue}{-2};\color{green}{5}) \) | \(\displaystyle \color{green}{5}=-2\cdot (\color{blue}{-2})+6\) \(\displaystyle 5=10\) | қате |
Демек, тек \(\displaystyle b\) түзуінің нүктесі \(\displaystyle y=-2x+6{\small ,}\) теңдеуін қанағаттандырады, сондықтан бұл түзу осы функцияның графигі болып табылады.
Жауабы: \(\displaystyle b{\small } \)түзуі.