Теориясы: Сызықтық функцияның графигі

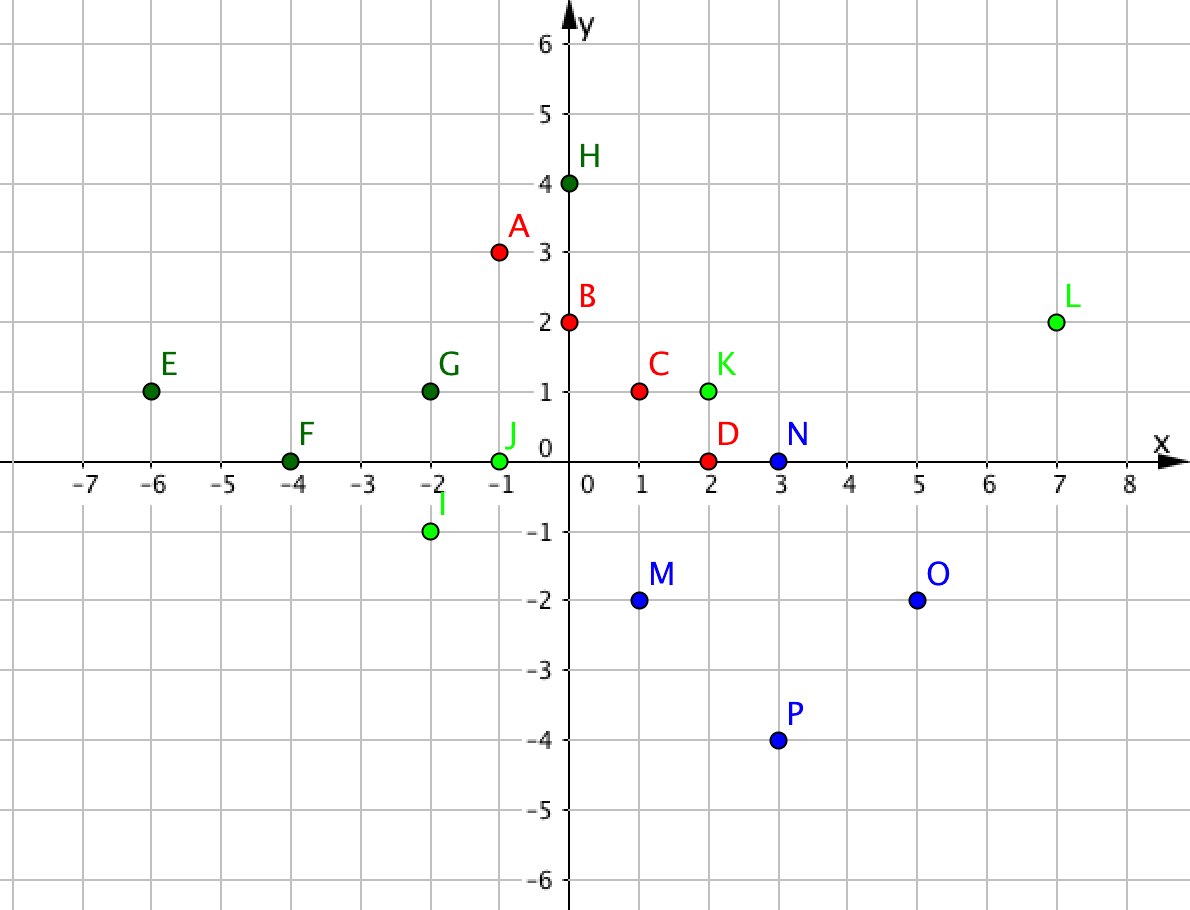
Алдымен әр жауап нұсқасының бірінші нүктесі \(\displaystyle y=-x+2{\small }\)сызықтық функциясының графигінде жатқанын тексереміз:

1. \(\displaystyle A,\, B,\,C,\,D\)

 \(\displaystyle A(\color{blue}{-1};\,\color{green}{3})\) нүктесі \(\displaystyle y=-x+2{\small ,}\)  сызықтық функциясының графигінде жатыр ,   себебі \(\displaystyle \color{green}{3}=-(\color{blue}{-1})+2{\small .}\)

2. \(\displaystyle E,\, F,\,G,\,H\)

 \(\displaystyle E(\color{blue}{-6};\,\color{green}{1})\)нүктесі \(\displaystyle y=-x+2{\small ,}\)  сызықтық функциясының графигінде жатпайды ,   себебі \(\displaystyle \color{green}{1} =\not 8=-(\color{blue}{-6})+2{\small .}\)

3. \(\displaystyle I,\, J,\,K,\,L\)

\(\displaystyle I(\color{blue}{-1};\,\color{green}{-2})\) нүктесі \(\displaystyle y=-x+2{\small ,}\) сызықтық функциясының графигінде жатпайды ,   себебі \(\displaystyle \color{green}{-2} =\not 3=-(\color{blue}{-1})+2{\small .}\)

4. \(\displaystyle M,\, N,\,O,\,P\)

 \(\displaystyle M(\color{blue}{-2};\,\color{green}{1})\) нүктесі \(\displaystyle y=-x+2{\small ,}\)  сызықтық функциясының графигінде жатпайды ,   себебі \(\displaystyle \color{green}{-2} =\not 1=-\color{blue}{1}+2{\small .}\)

Демек, берілген түзуде \(\displaystyle A,\, B,\,C,\,D{\small , }\) нүктелерінің бірінші тобы ғана болуы мүмкін.

Осы топтың қалған нүктелерін тексерейік:

Жауабы: \(\displaystyle A,\, B,\,C,\,D\) нүктелері \(\displaystyle y=-x+2{\small .}\)сызықтық функциясының графигінде жатыр.