\(\displaystyle OC\) сәулесі \(\displaystyle ∠ AOB\) жазыңқы бұрышын \(\displaystyle ∠ AOC\) және \(\displaystyle ∠ BOC\) екі іргелес бұрышқа бөледі, сондықтан \(\displaystyle ∠ AOC\) бұрышы \(\displaystyle ∠ BOC\) бұрышынан \(\displaystyle 3\) есе үлкен болады . \(\displaystyle ∠ AOC\) және \(\displaystyle ∠ BOC\) бұрыштарын табыңыз.
\(\displaystyle ∠ AOC=\)\(\displaystyle ^{\circ},\) \(\displaystyle ∠ BOC=\)\(\displaystyle ^{\circ}\)
Жазыңқы және іргелес бұрыштар
Егер түзуде нүктені белгілесе, онда осы нүктеден шығатын екі сәуле пайда болады. Бұл сәулелер жазықтықты екіге бөледі, олардың әрқайсысы жазыңқы бұрыш деп аталады. Суретте \(\displaystyle ∠ ABC\) жазыңқы бұрышы көрсетілген.
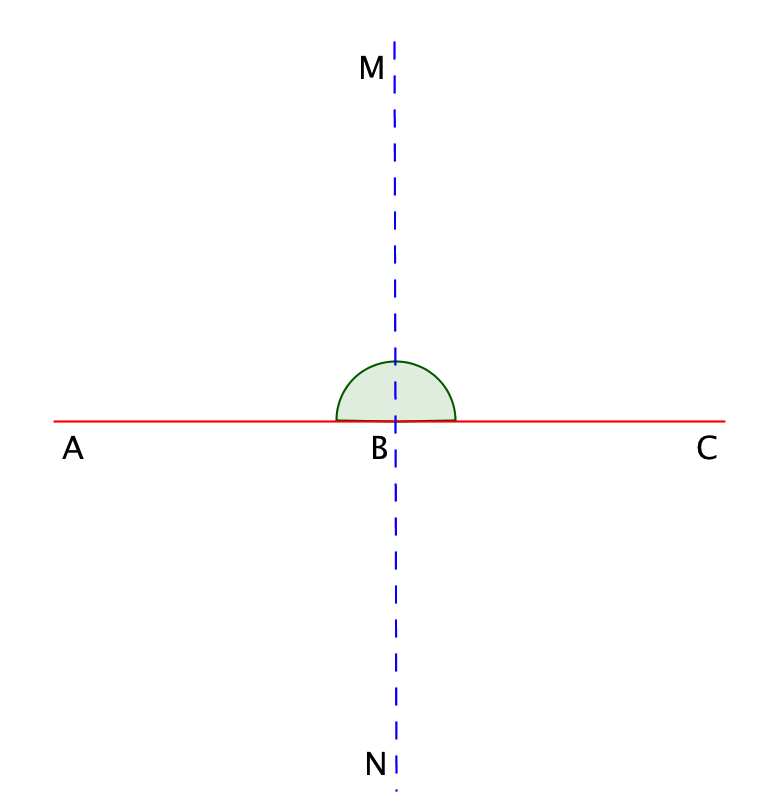
Жазыңқы бұрыш \(\displaystyle 180\) градусты құрайды: \(\displaystyle ∠ ABC=180^{\circ}\)
\(\displaystyle ∠ ABC\) жазыңқы бұрышының ішінде \(\displaystyle BD\) сәулесі жүргізілген . Ол жазыңқы бұрышты екі бұрышқа бөледі: \(\displaystyle ∠ ABD\) және \(\displaystyle ∠ DBC\), олар іргелес бұрыштар деп аталады.
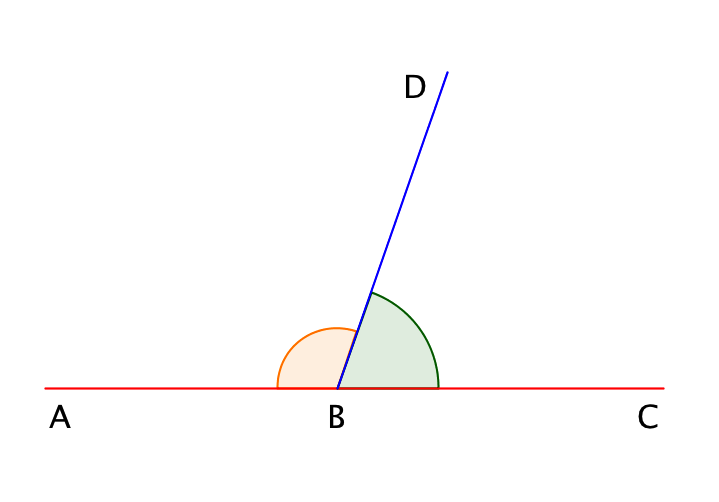
Іргелес бұрыштардың қосындысы \(\displaystyle 180^{\circ}\) тең:
\(\displaystyle ∠ ABD+∠ DBC=∠ ABС=180^{\circ}.\)
\(\displaystyle ∠ AOC\) және \(\displaystyle ∠ BOC\) бұрыштары іргелес болғандықтан, олардың қосындысы \(\displaystyle 180^{\circ}\) тең:
\(\displaystyle ∠ AOC+∠ BOC=180^{\circ}\).
\(\displaystyle x\) - \(\displaystyle ∠ BOC\) бұрышының шамасы болсын, сонда \(\displaystyle 3\cdot x\) - \(\displaystyle ∠ AOC\) бұрышының шамасы.
Осылайша,
\(\displaystyle x+3\cdot x=180^{\circ},\)
\(\displaystyle 4\cdot x=180^{\circ},\)
\(\displaystyle x=45^{\circ}.\)
Демек, \(\displaystyle ∠ BOC=45^{\circ},\) \(\displaystyle ∠ AOC=3\cdot 45^{\circ}=135^{\circ}.\)
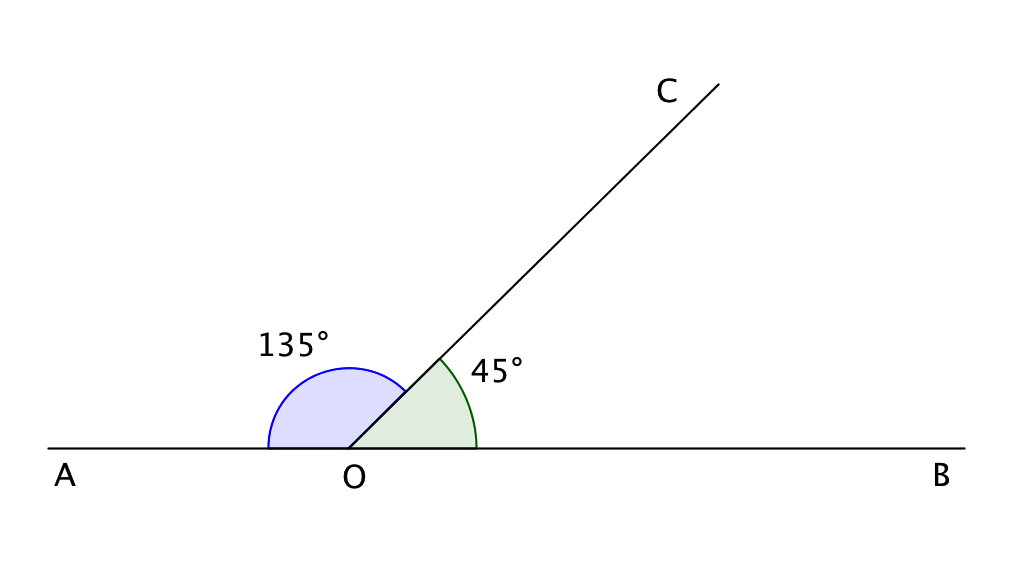
Жауабы: \(\displaystyle ∠ AOC=135^{\circ},\) \(\displaystyle ∠ BOC=45^{\circ}.\)