Суретте көрсетілген бұрыштардың қайсысы жазыңқы болып табылады?

Жазыңқы, тік, сүйір, доғал бұрыштар
Егер түзуде нүктені белгілесе, онда осы нүктеден шығатын екі сәуле пайда болады. Бұл сәулелер жазықтықты екіге бөледі, олардың әрқайсысы жазыңқы бұрыш деп аталады. Суретте ∠ ABC жазыңқы бұрышы көрсетілген.
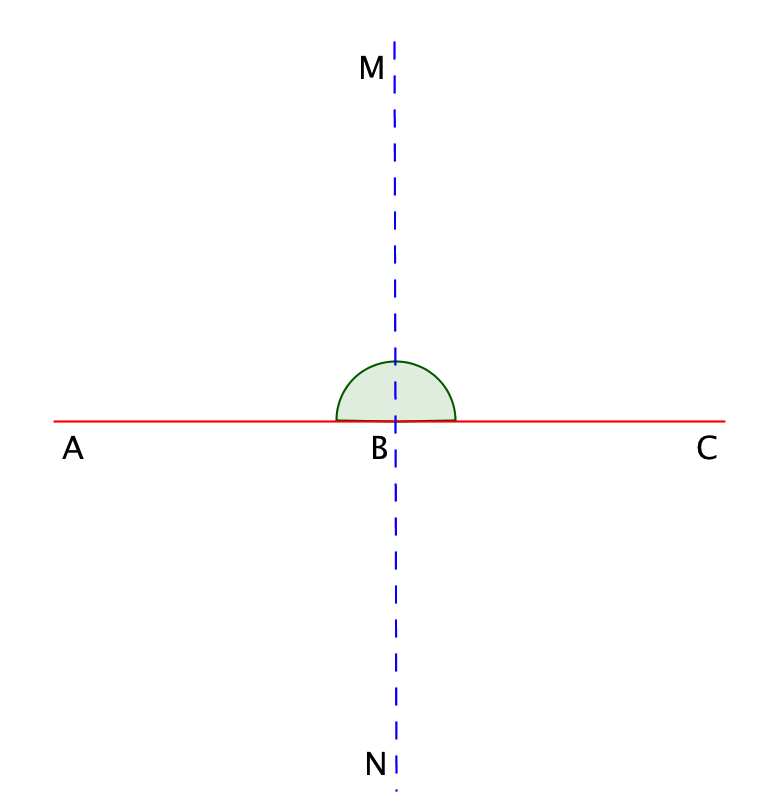
Жазыңқы бұрыш \(\displaystyle 180\) градусты құрайды: \(\displaystyle ∠ ABC=180^{\circ}\) .
Қағаз парағын BA және BC сәулелері сәйкес келетін етіп аударамыз және парақты тегістейміз. Сонда \(\displaystyle MN\) ию сызығы жазыңқы бұрыштардың әрқайсысын екі тең бұрышқа бөледі, олардың әрқайсысы тік бұрыш деп аталады.
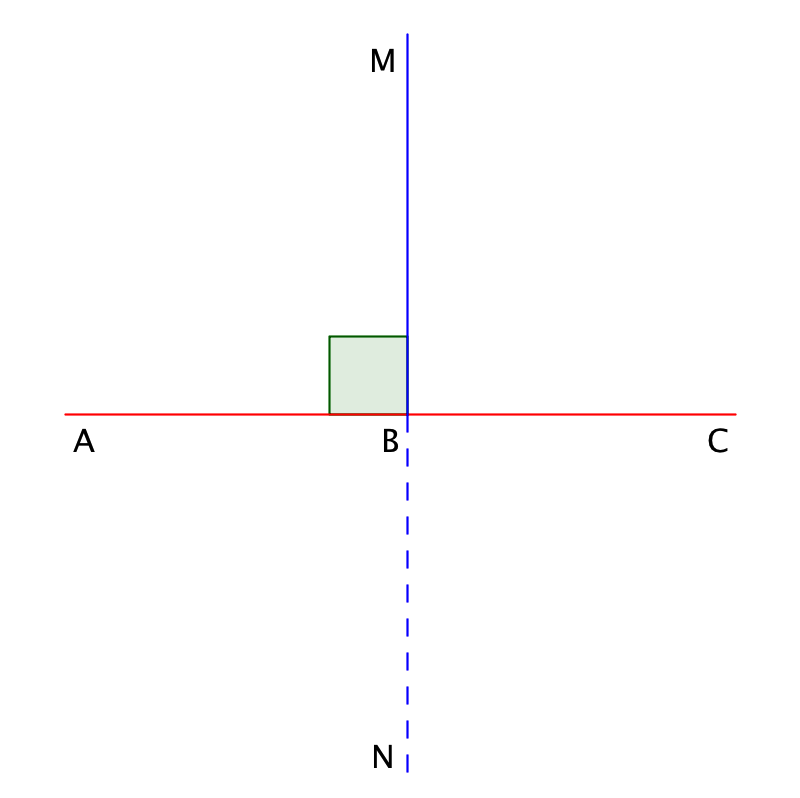
Тік бұрыш - жазыңқы бұрыштың жартысы. Бұл \(\displaystyle 90\) градусты құрайды: \(\displaystyle ∠ ABM=90^{\circ}\)
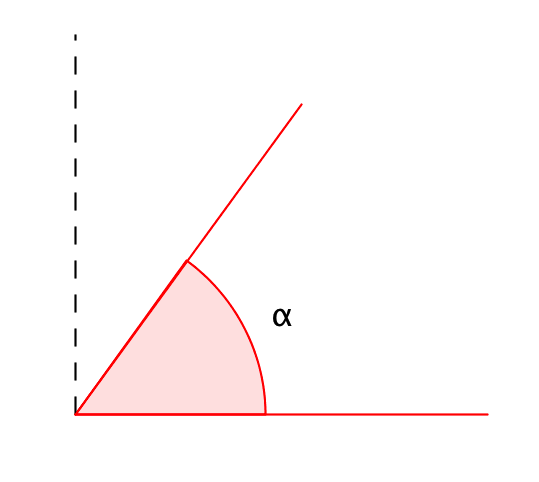
Егер \(\displaystyle \alpha\) бұрышы тік бұрыштан кіші болса, онда ол сүйір бұрыш деп аталады: \(\displaystyle \alpha<90^{\circ}\).
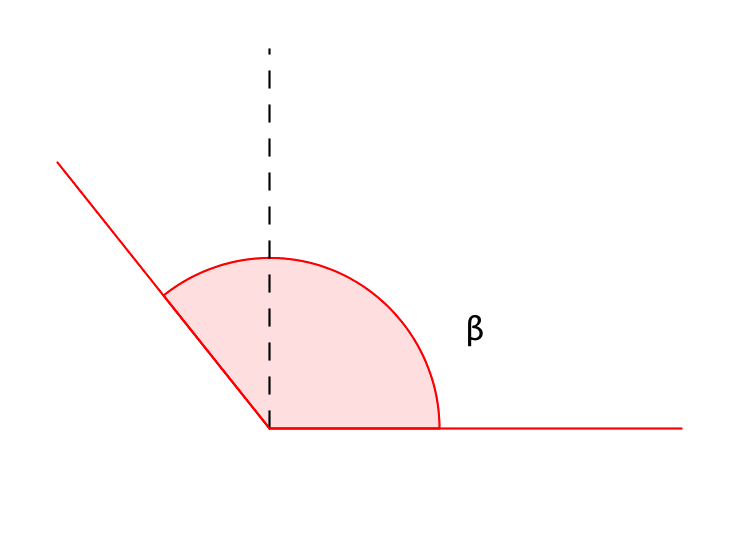
Егер \(\displaystyle \beta\) бұрышы тік бұрыштан үлкен, бірақ жазыңқы бұрыштан кіші болса, онда ол доғал бұрыш деп аталады: \(\displaystyle 90^{\circ}<\beta<180^{\circ}\)
Біздің жағдайда \(\displaystyle ∠ ACD\) бұрышы жазыңқы болып табылады - ол бүкіл жазықтықты екіге бөледі және оның мәні \(\displaystyle 180^{\circ}\) құрайды.

Жауабы: \(\displaystyle ∠ ACD\).