Какая из точек \(\displaystyle A(5)\), \(\displaystyle B(100)\), \(\displaystyle C(56)\) или \(\displaystyle D(37)\) расположена на координатном луче правее всех?
Чем больше расстояние от точки \(\displaystyle O(0)\) до данной точки, расположенной на координатном луче, тем больше ее координата и, следовательно, тем правее находится эта точка относительно всех остальных.
Изобразим на координатном луче точки \(\displaystyle A(5)\), \(\displaystyle B(100)\), \(\displaystyle C(56)\) и \(\displaystyle D(37)\). Координаты точек слишком велики для того чтобы показать на рисунке единичный отрезок – он будет слишком мал, поэтому его показывать не будем.
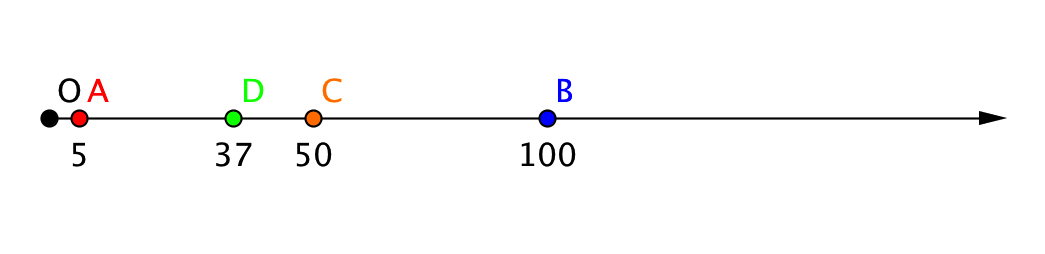
Таким образом, из всех точек наибольшую координату имеет точка \(\displaystyle B\): \(\displaystyle B(100)\), следовательно, именно она находится на большем расстоянии от точки \(\displaystyle O(0)\) и расположена на координатном луче правее всех остальных трех точек.
Ответ: точка \(\displaystyle B\).