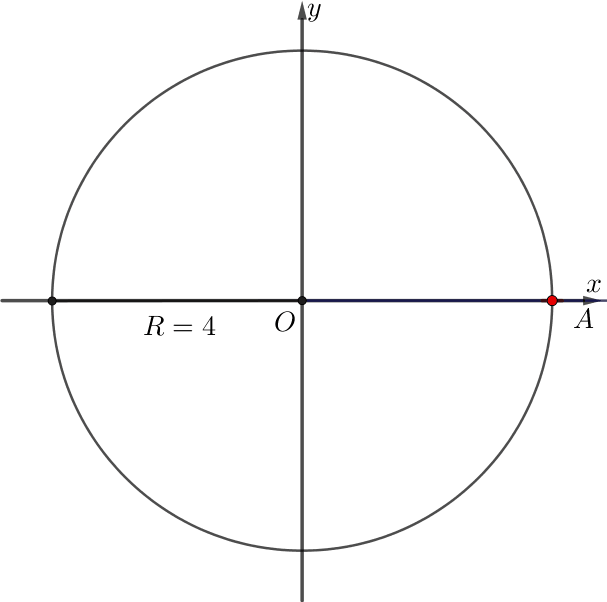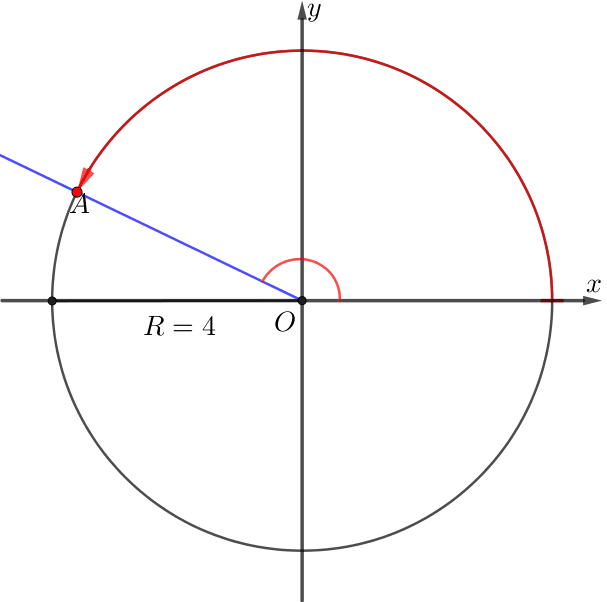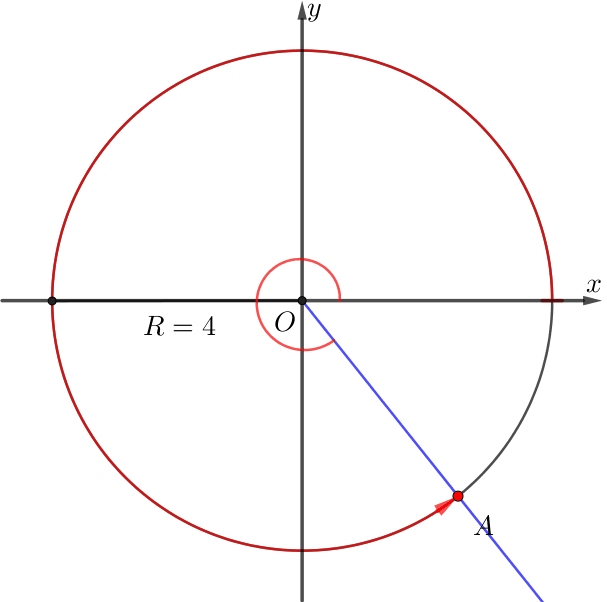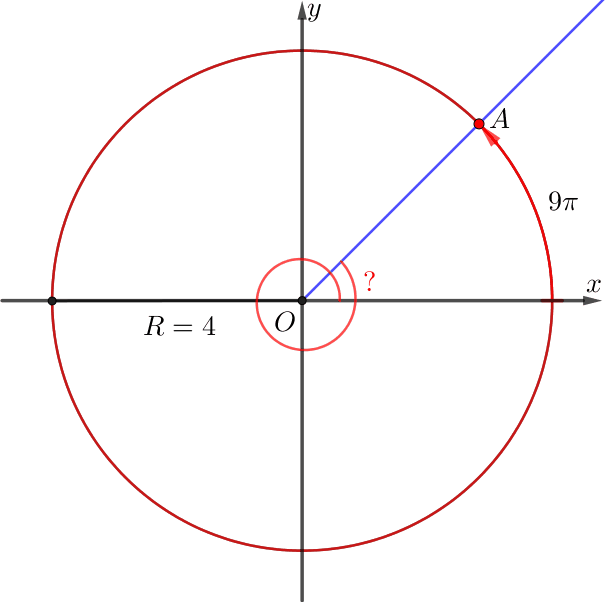
\(\displaystyle OA\) сәулесі \(\displaystyle \alpha{\small}\) бұрышына бұрылды. \(\displaystyle A\) нүктесі барлық уақытта \(\displaystyle R=4{\small}\) радиусының шеңберімен қозғалды. Егер \(\displaystyle A{\small }\) нүктесінің жүріп өткен жолы \(\displaystyle 9\pi{\small}\) тең болса, \(\displaystyle \alpha\) радианмен есептегенде қаншаға тең болады?
Бір радиан болатын орталық бұрыш - ұзындығы \(\displaystyle R{\small} \) радиусқа тең болатын доғаға тіреледі.
Сонда, сәуле \(\displaystyle 1\) радианға айналған (бұрылған) кезде, \(\displaystyle A{\small}\) нүктесі \(\displaystyle R{\small}\) радиусының шеңберімен қозғала отырып \(\displaystyle R{\small}\) жол жүреді.
Демек, сәуле \(\displaystyle \alpha\) радианға бұрылу кезінде :
\(\displaystyle A{\small}\) нүктесінің жүріп өткен жолы \(\displaystyle \alpha\cdot R{\small}\) тең болады.
Шарт бойынша, \(\displaystyle A{\small}\) нүктесінің жүріп өткен жолы \(\displaystyle 9\pi\) және \(\displaystyle R=4{\small}\) тең.
Демек,
\(\displaystyle 9\pi=\alpha\cdot 4{\small.}\)
Осы жерде\(\displaystyle \alpha{\small}\) табамыз:
\(\displaystyle \alpha=\frac{9\pi}{4}{\small.}\)
Жауабы: \(\displaystyle \frac{9\pi}{4}\) радиан.