\(\displaystyle A\) нүктесін координаталары
\(\displaystyle (0{,}8;\, \sin(0{,}8)){\small}\) болатын нүктеге көшіреміз.
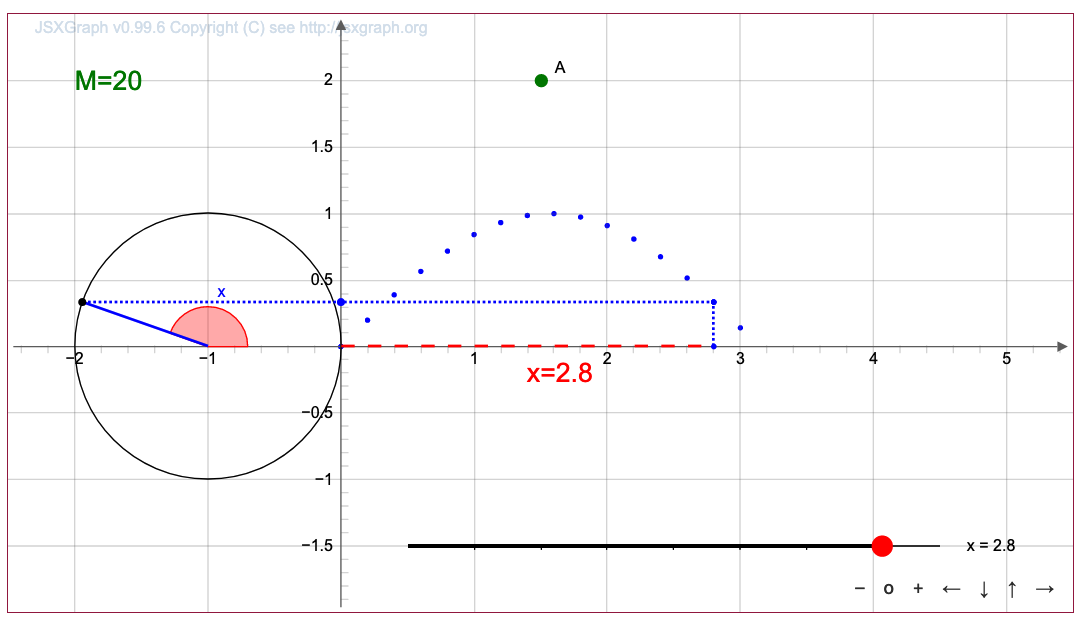
\(\displaystyle (0{,}8;\, \sin(0{,}8))\) нүктесінің орналасуын табу үшін бірлік шеңберді қолданыңыз.
Тексеру мәнін енгізіңіз:
\(\displaystyle \color{green}{M}=\)
Координатасы \(\displaystyle x=0{,}8\) бірлік болатын нүкте алу үшін, \(\displaystyle x\)-ті \(\displaystyle 0{,}8\)-ге орналастыру керек.
Онда құрылымы бойынша шеңбердегі нүкте үзындығы \(\displaystyle 0{,}8\) бірлік болатын доғаны өтеді.
Осылайша, \(\displaystyle 0{,}8 \) радианға тең бұрыш алдық.
Бірлік шеңбердегі нүкте \(\displaystyle \sin(0{,}8)\)-ге тең \(\displaystyle y\) координатасына ие болады.

Құрылымы бойынша, көк нүктенің координатасы \(\displaystyle y\) шеңбердегі нүктенің координатасымен бірдей, яғни \(\displaystyle \sin(0{,}8)\) тең.
Осылайша берілген сызбада көк нүктенің:
- \(\displaystyle x\)-ке тең, \(\displaystyle \rm OX\) осі бойынша координатасы ;
- шеңбердегі нүктенің ординатасына, яғни \(\displaystyle \sin(x){\small }\) тең, \(\displaystyle \rm OY\) осі бойынша координатасы бар.
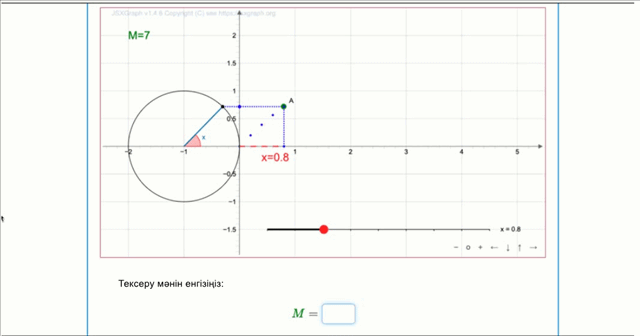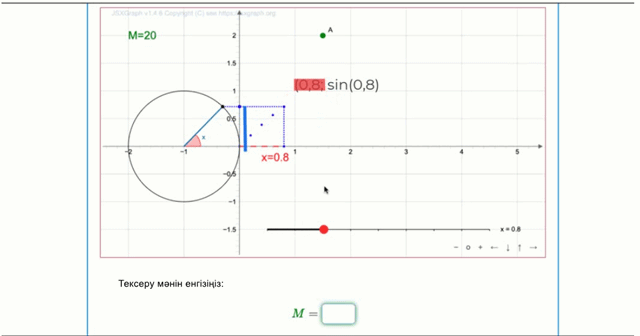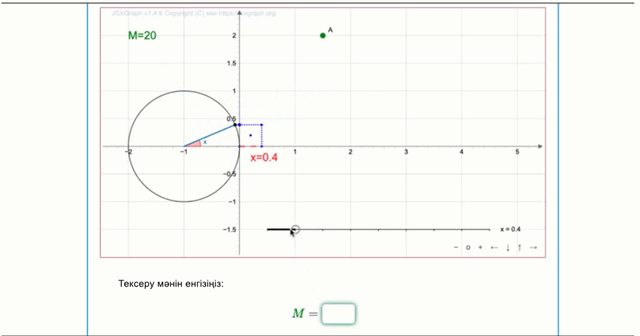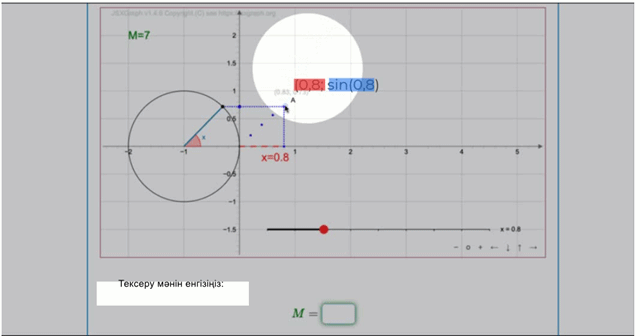
Егер жүгірткі \(\displaystyle x=0{,}8\) жағдайында болса, координатасы \(\displaystyle (0{,}8;\,\sin(0{,}8)){\small}\) болатын көк нүкте аламыз.
Әрі қарай \(\displaystyle A\) нүктесін табылған нүктеге жылжыту арқылы \(\displaystyle M=7\) нүктесін аламыз.