Так как значения синуса лежат на оси \(\displaystyle \rm OY{ \small ,}\) то пересечем прямую \(\displaystyle y=-\frac{\sqrt{3}}{2}\) и тригонометрическую окружность:
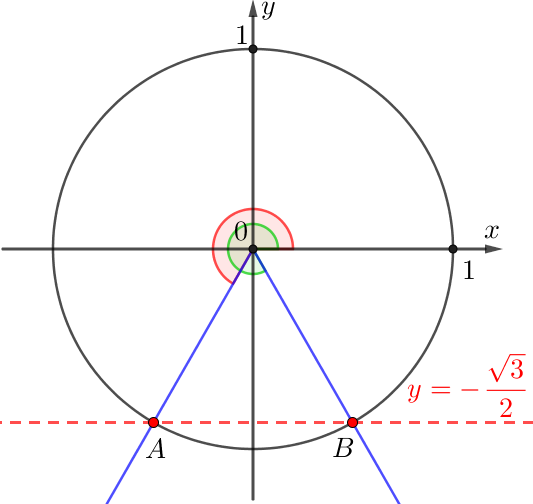
Получаем два набора решений, соответствующих двум точкам.
Угол поворота луча, соответствующего точке \(\displaystyle A{\small,}\) равен \(\displaystyle \frac{4\pi}{3}\) радиан.
Согласно таблице значений тригонометрических функций \(\displaystyle \sin\left(\frac{\pi}{3}\right)=\frac{\sqrt{3}}{2}{\small.}\)
Точка \(\displaystyle A\) центрально-симметрична точке \(\displaystyle A_1{\small,}\) соответствующей повороту на \(\displaystyle \frac{\pi}{3}{\small:}\)
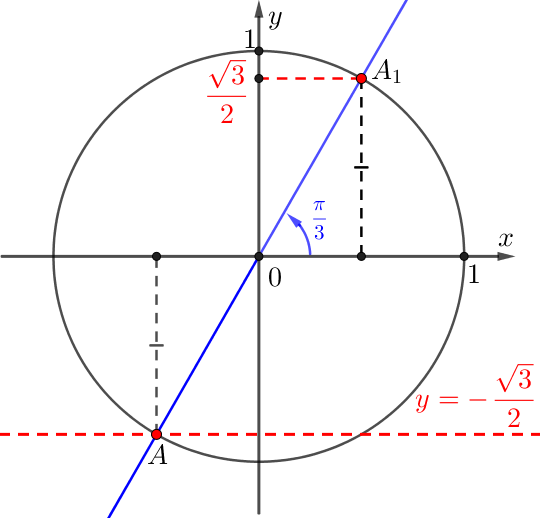
Значит, угол поворота луча \(\displaystyle OA\) равен \(\displaystyle \pi+\frac{\pi}{3}=\frac{4\pi}{3}{\small:}\)
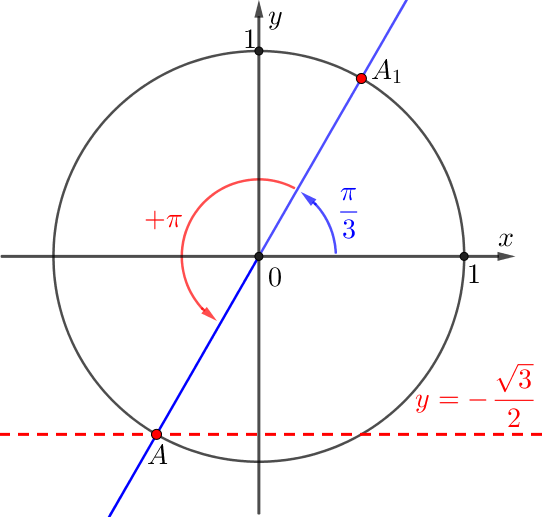
Таким образом, получаем первый набор решений:
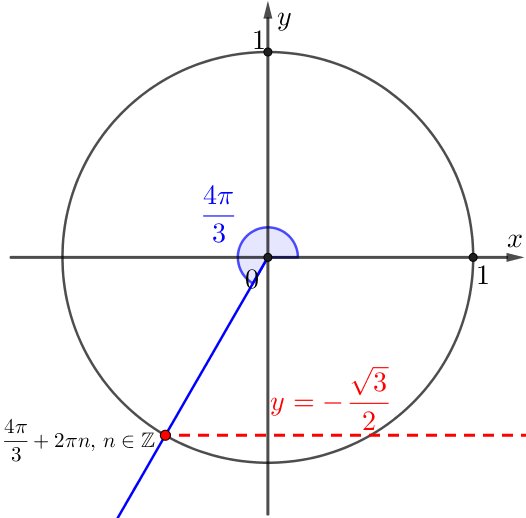 | \(\displaystyle x_1=\frac{4\pi}{3}+2\pi n, \, n\in \mathbb{Z}{ \small .}\) |
Угол поворота луча, соответствующего точке \(\displaystyle B{\small,}\) равен \(\displaystyle \frac{5\pi}{3}\) радиан.
Согласно таблице значений тригонометрических функций \(\displaystyle \sin\left(\frac{\pi}{3}\right)=\frac{\sqrt{3}}{2}{\small.}\)
Точка \(\displaystyle B\) симметрична относительно оси \(\displaystyle \rm OX\) точке \(\displaystyle B_1{\small,}\) соответствующей повороту на \(\displaystyle \frac{\pi}{3}{\small:}\)
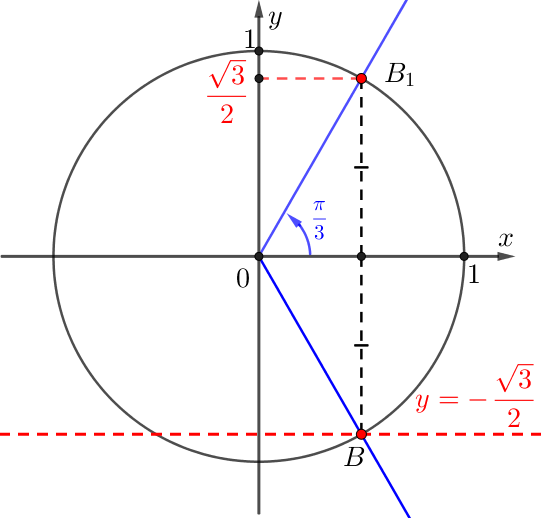
Значит, угол поворота луча \(\displaystyle OB\) равен \(\displaystyle -\frac{\pi}{3}\) или \(\displaystyle 2\pi-\frac{\pi}{3}=\frac{5\pi}{3}{\small:}\)
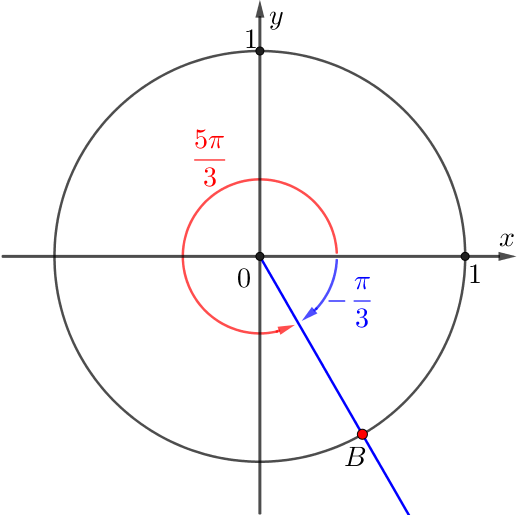
Таким образом, получаем второй набор решений:
 | \(\displaystyle x_1=\frac{5\pi}{3}+2\pi n, \, n\in \mathbb{Z}{ \small .}\)
|
Ответ: \(\displaystyle x_1=\frac{4\pi}{3}+2\pi n, \, n\in \mathbb{Z}\) и \(\displaystyle x_2=\frac{5\pi}{3}+2\pi n, \, n\in \mathbb{Z}{ \small .}\)