Найдите уравнение прямой:
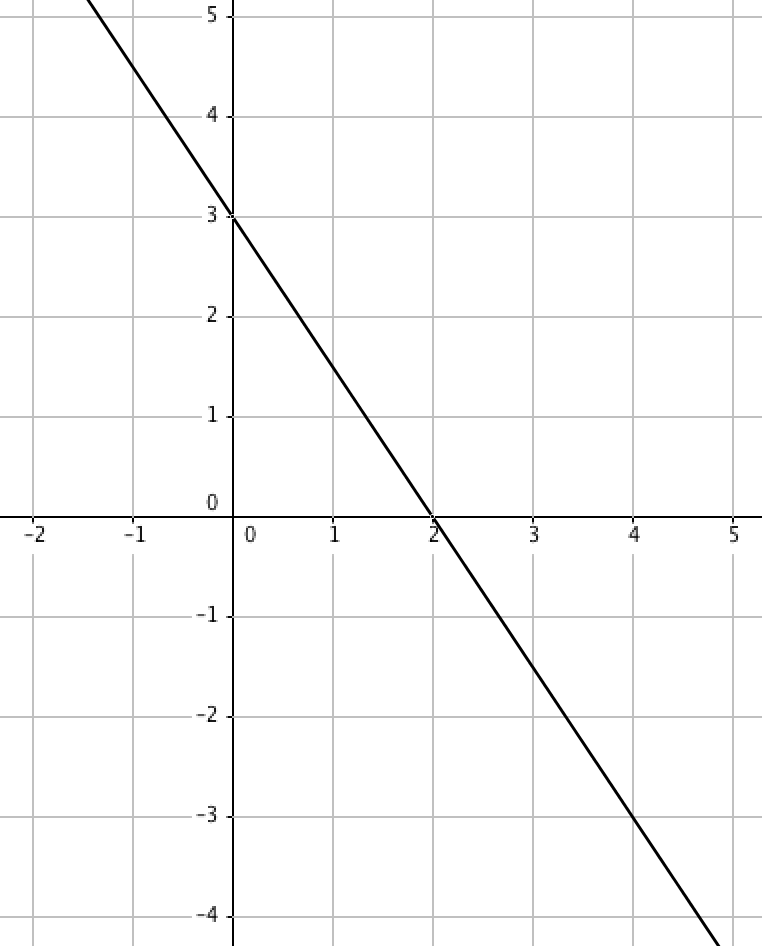
\(\displaystyle y=\)
Выберем точки \(\displaystyle A\) и \(\displaystyle B\) на прямой, для удобства, с целыми координатами:
Подставим координаты точек \(\displaystyle A(0;3)\) и \(\displaystyle B(2;0)\) в уравнение прямой \(\displaystyle y=kx+b\,{\small . } \)
Точка \(\displaystyle A(\color{blue}{ 0};\color{green}{3}) \) с координатами \(\displaystyle x=\color{blue}{ 0}\) и \(\displaystyle y=\color{green}{ 3}{\small , }\) поэтому
\(\displaystyle \color{green}{3}=k\cdot \color{blue}{ 0}+b \)
или, что то же самое,
\(\displaystyle b=3{\small . }\)
Точка \(\displaystyle B(\color{blue}{ 2};\color{green}{ 0}) \) с координатами \(\displaystyle x=\color{blue}{ 2}\) и \(\displaystyle y=\color{green}{ 0}{\small , }\) поэтому
\(\displaystyle \color{green}{ 0}=k\cdot \color{blue}{ 2}+b \)
или, что то же самое,
\(\displaystyle 2k+b=0{\small . } \)
Мы получили два уравнения для коэффициентов \(\displaystyle k \) и \(\displaystyle b, \) и можем записать систему уравнений:
\(\displaystyle \left\{ \begin{aligned} b&=3{\small , }\\ 2k+b&=0{\small . } \end{aligned} \right. \)
Решим эту систему.
Таким образом, \(\displaystyle k=-\frac{ 3}{ 2}\) и \(\displaystyle b=3{\small . } \)
Подставляя найденные значения для \(\displaystyle k \) и \(\displaystyle b \) в уравнение прямой \(\displaystyle y=kx+b{\small , } \) получаем:
\(\displaystyle y=-\frac{ 3}{ 2}x+3{\small . } \)
Ответ: \(\displaystyle y={\bf -\frac{ 3}{ 2}x+3}{\small . } \)