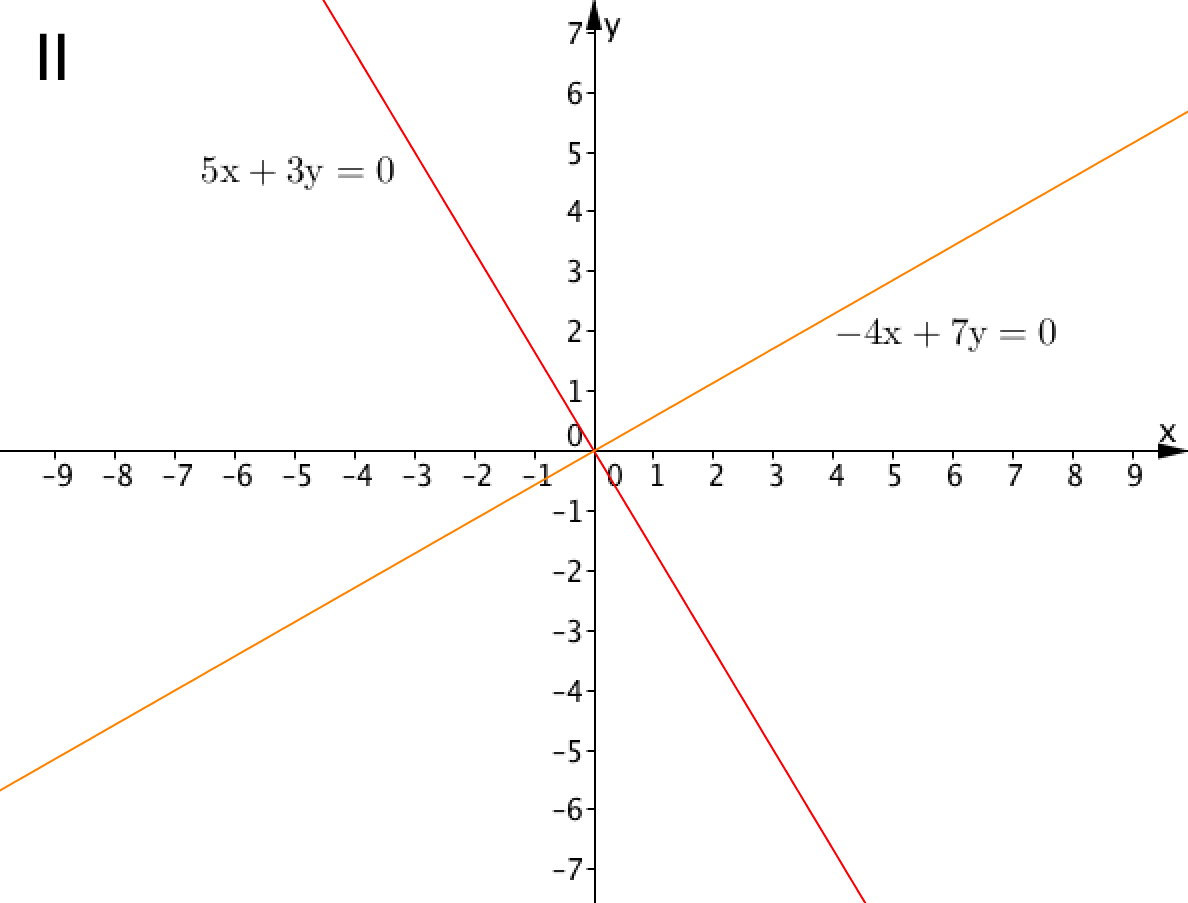
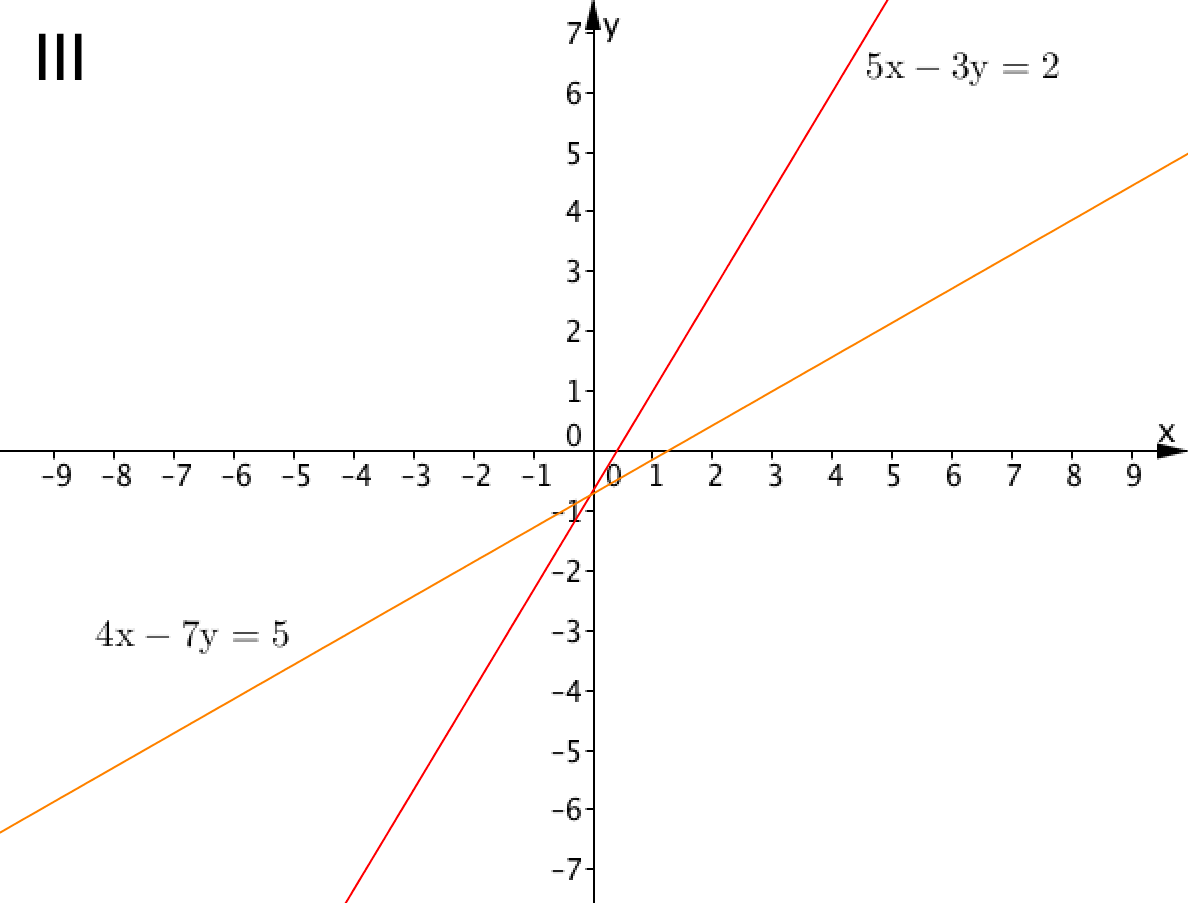
Выберите пару прямых, точка пересечения которых соответствует решению системы линейных уравнений:
\(\displaystyle \left\{ \begin{aligned} 5x+3y&=-2\\ -4x+7y&=5 \end{aligned} \right. \)
|
|
|
|
С геометрической точки зрения, решением системы уравнений
\(\displaystyle \left\{ \begin{aligned} 5x+3y&=-2\\ -4x+7y&=5 \end{aligned} \right. \)
является точка с координатами \(\displaystyle (x_0;\, y_0){\small ,}\) которая одновременно лежит на прямой \(\displaystyle 5x+3y=-2\)
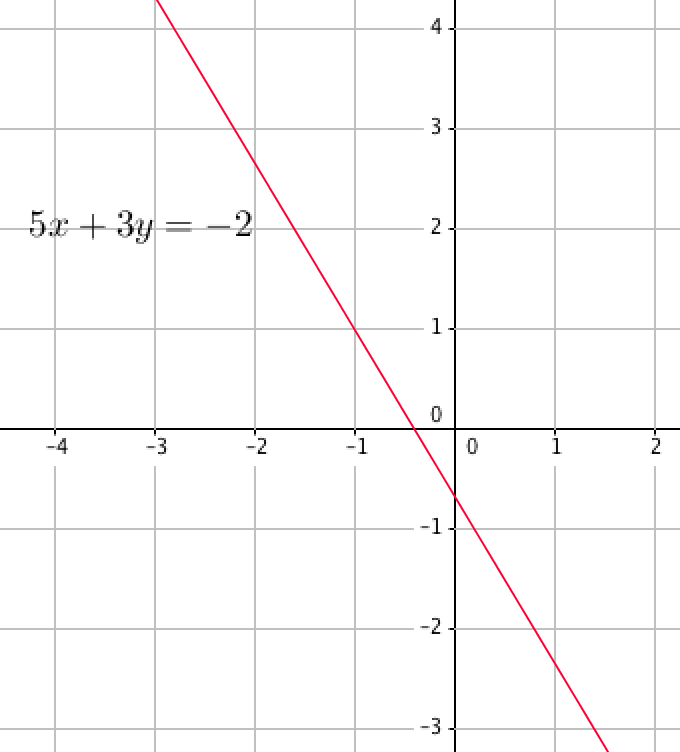
и прямой \(\displaystyle -4x+7y=5\)

Этой точкой является точка пересечения прямых \(\displaystyle 5x+3y=-2\) и \(\displaystyle -4x+7y=5{\small .}\)
Таким образом, правильным ответом является вариант \(\displaystyle {\rm I}{\small .}\)
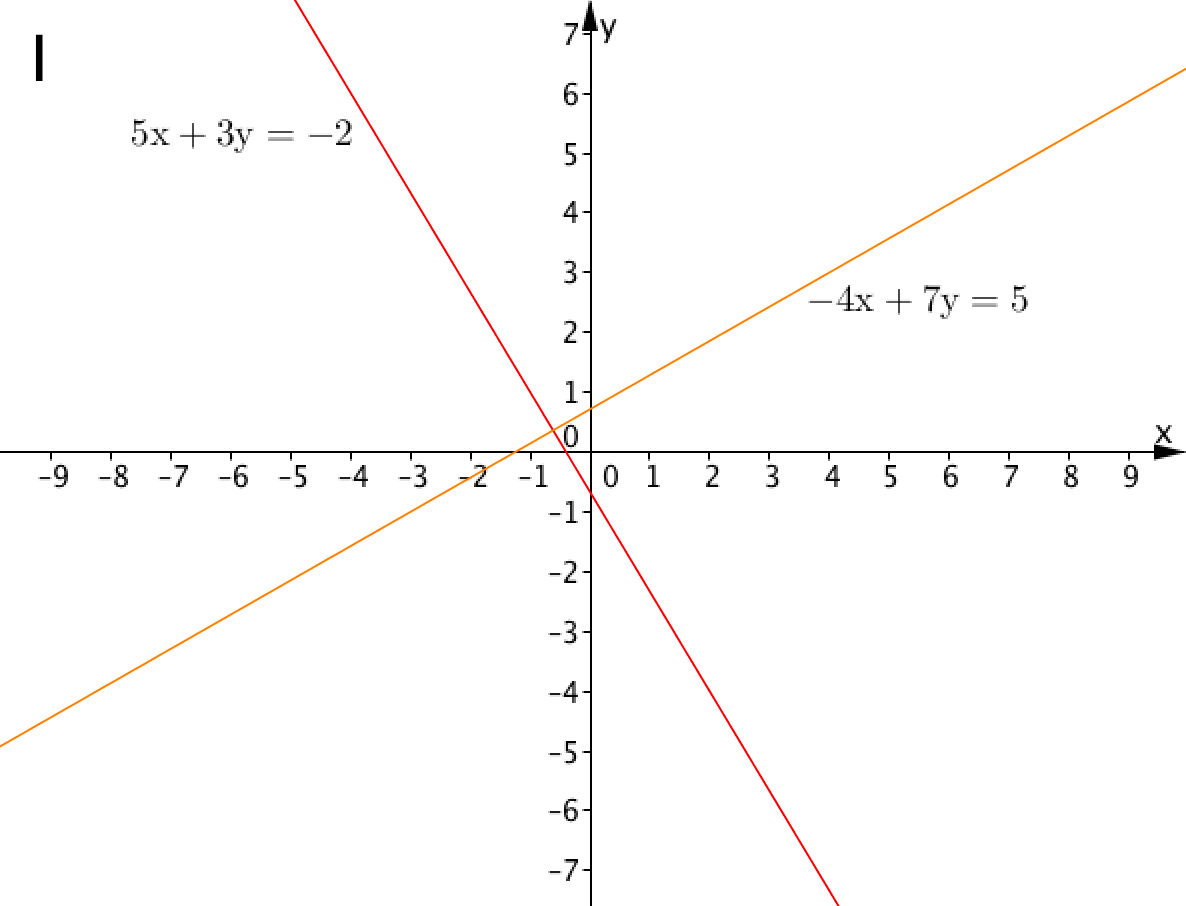
Ответ: \(\displaystyle {\rm I}{\small .}\)