График квадратичной функции \(\displaystyle y=-\frac{ x^2}{0{,}4}\) получен из квадратичной функции \(\displaystyle y=-x^2\)
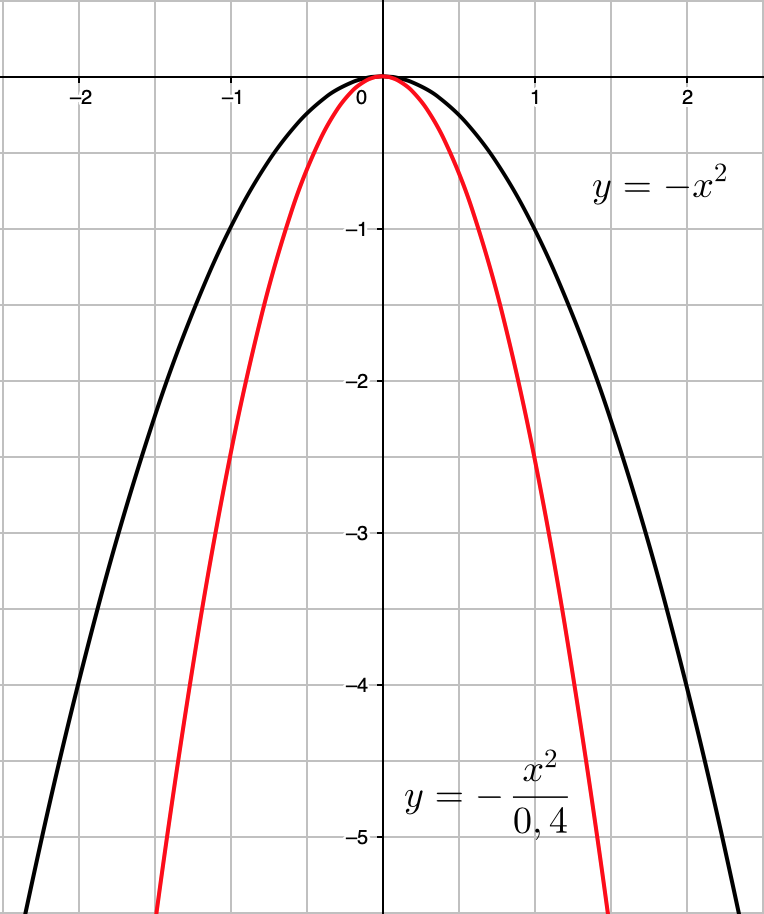
Графиком параболы \(\displaystyle y=\color{blue}{ -x^2}\) является множество точек вида \(\displaystyle \{(\color{blue}{ x};\, \color{blue}{ -x^2}) \}\) для всех действительных чисел \(\displaystyle x{\small .}\)
Графиком параболы \(\displaystyle y=\color{red}{ -\frac{x^2}{0{,}4}}=\color{red}{ \frac{ -x^2}{\phantom{1}\frac{ 4}{ 10 }\phantom{1}}}=\color{red}{ -2{,}5x^2}\) является множество точек вида \(\displaystyle \{(\color{red}{ x};\, \color{red}{ -2{,}5x^2}) \}\) для всех действительных чисел \(\displaystyle x{\small .}\)
Растяжение вдоль оси \(\displaystyle \rm OY \) параболы \(\displaystyle y=-x^2 \) в \(\displaystyle k \) раз – это умножение координаты \(\displaystyle y \) для всех точек \(\displaystyle (x; -x^2) \) графика на \(\displaystyle k \) для \(\displaystyle k>1{\small .}\)
Сравним, как изменилась координата \(\displaystyle y \) для парабол \(\displaystyle y=\color{blue}{-x^2} \) и \(\displaystyle y=\color{red}{-2{,}5x^2}{\small :} \)
\(\displaystyle \color{blue}{-x^2}\longrightarrow\,\color{red}{-2{,}5x^2} \)
То есть было \(\displaystyle \color{blue}{ -x^2}{ \small ,} \) а стало \(\displaystyle \color{red}{ -2.5x^2}{\small .} \) Значит, координата \(\displaystyle y \) умножалась на
\(\displaystyle \frac{ \color{red}{ -2{,}5x^2}}{ \color{blue}{ -x^2}}=2{,}5{\small .} \)
Так как \(\displaystyle 2>1{ \small ,} \) то это означает, что координата \(\displaystyle y \) умножалась на \(\displaystyle 2{,}5>1{ \small .} \)
Значит, имело место растяжение графика параболы \(\displaystyle y=-x^2 \) вдоль оси \(\displaystyle \rm OY \) в \(\displaystyle 2{,}5\) раза.
Ответ: график параболы \(\displaystyle y=-x^2 \) растянули вдоль оси \(\displaystyle \rm OY \) в \(\displaystyle 2{,}5\) раза.