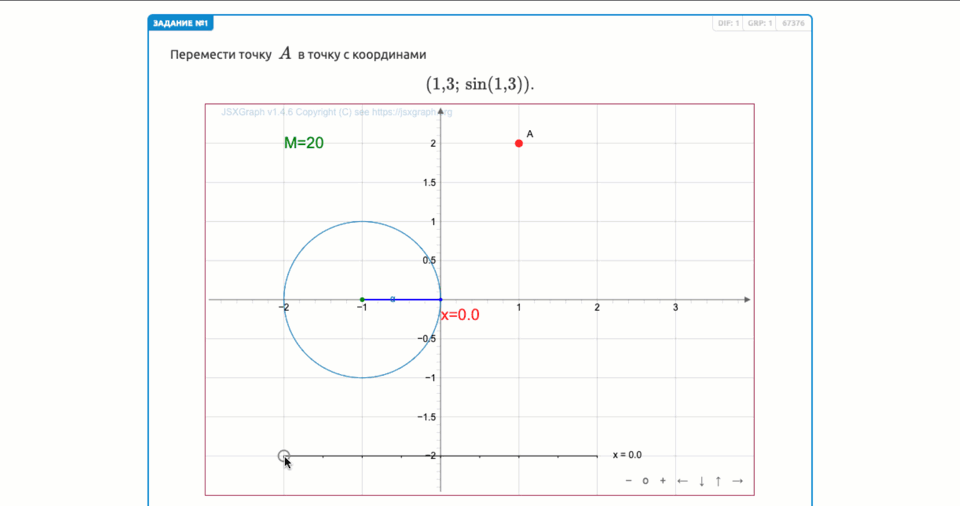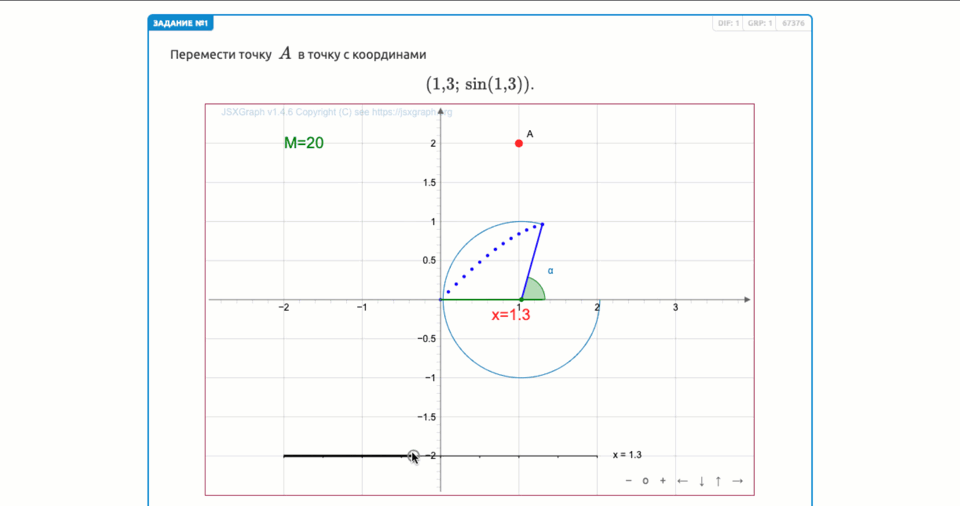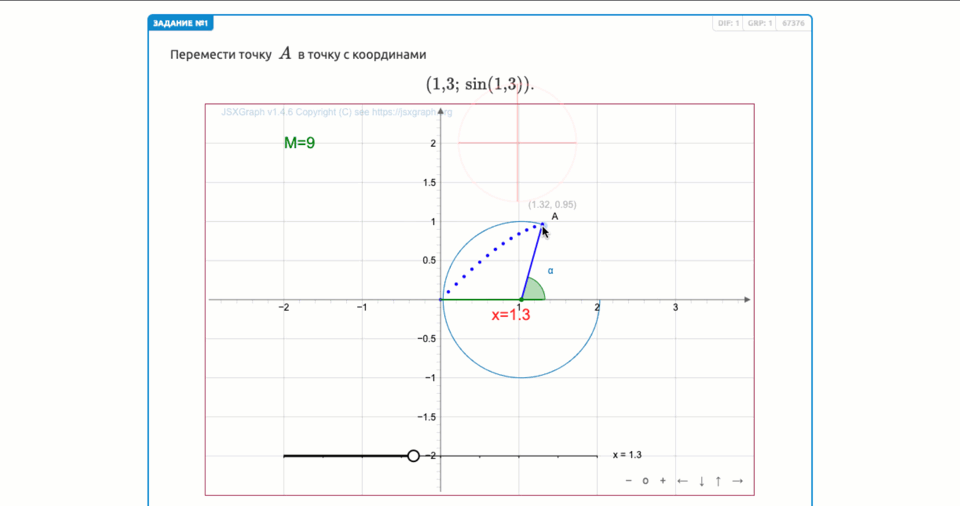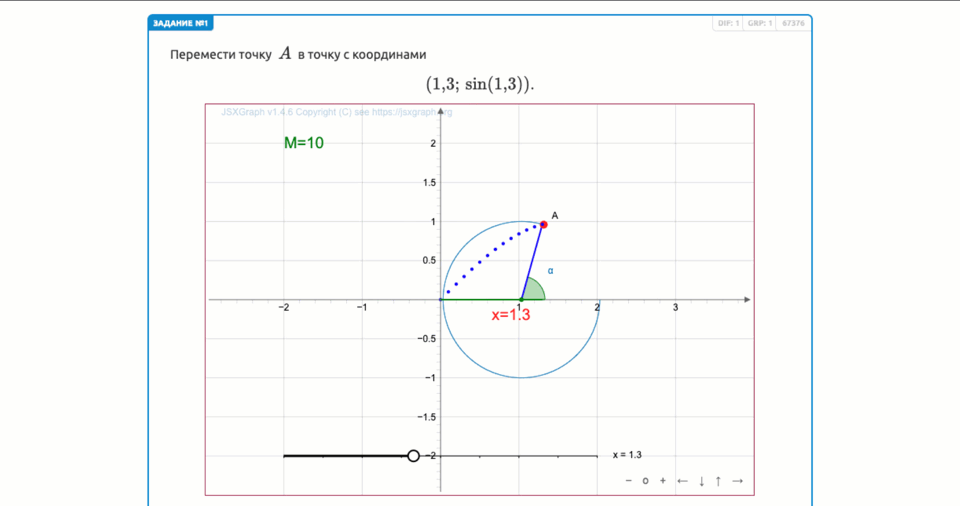
Переместите точку \(\displaystyle A\) в точку с координатами
\(\displaystyle (1{,}3;\, \sin(1{,}3)){\small .}\)
Введите контрольное значение:
\(\displaystyle \color{green}{M}=\)
Чтобы получить точку с координатой \(\displaystyle x=1{,}3\) единиц, нужно переместить \(\displaystyle x\) в положение \(\displaystyle 1{,}3{\small .}\)
По построению длина исчезнувшей дуги на единичной окружности равна \(\displaystyle 1{,}3\) радиан.
То есть, мы получили угол, равный \(\displaystyle 1{,}3\) радиан.
Таким образом, при движении окружности точка на ней образует угол, равный \(\displaystyle 1{,}3\) радиан.
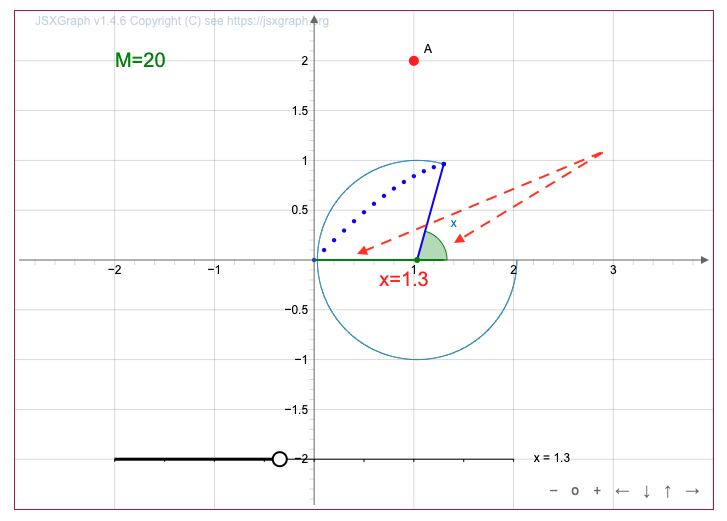
Так как точка лежит на единичной окружности, то координата \(\displaystyle y\) равна \(\displaystyle \sin(1{,}3){\small .}\)

Следовательно, мы получили точку с координатами
\(\displaystyle (1{,}3;\,\sin(1{,}3) ){\small .}\)
Контрольное значение \(\displaystyle M=10{\small .}\)
