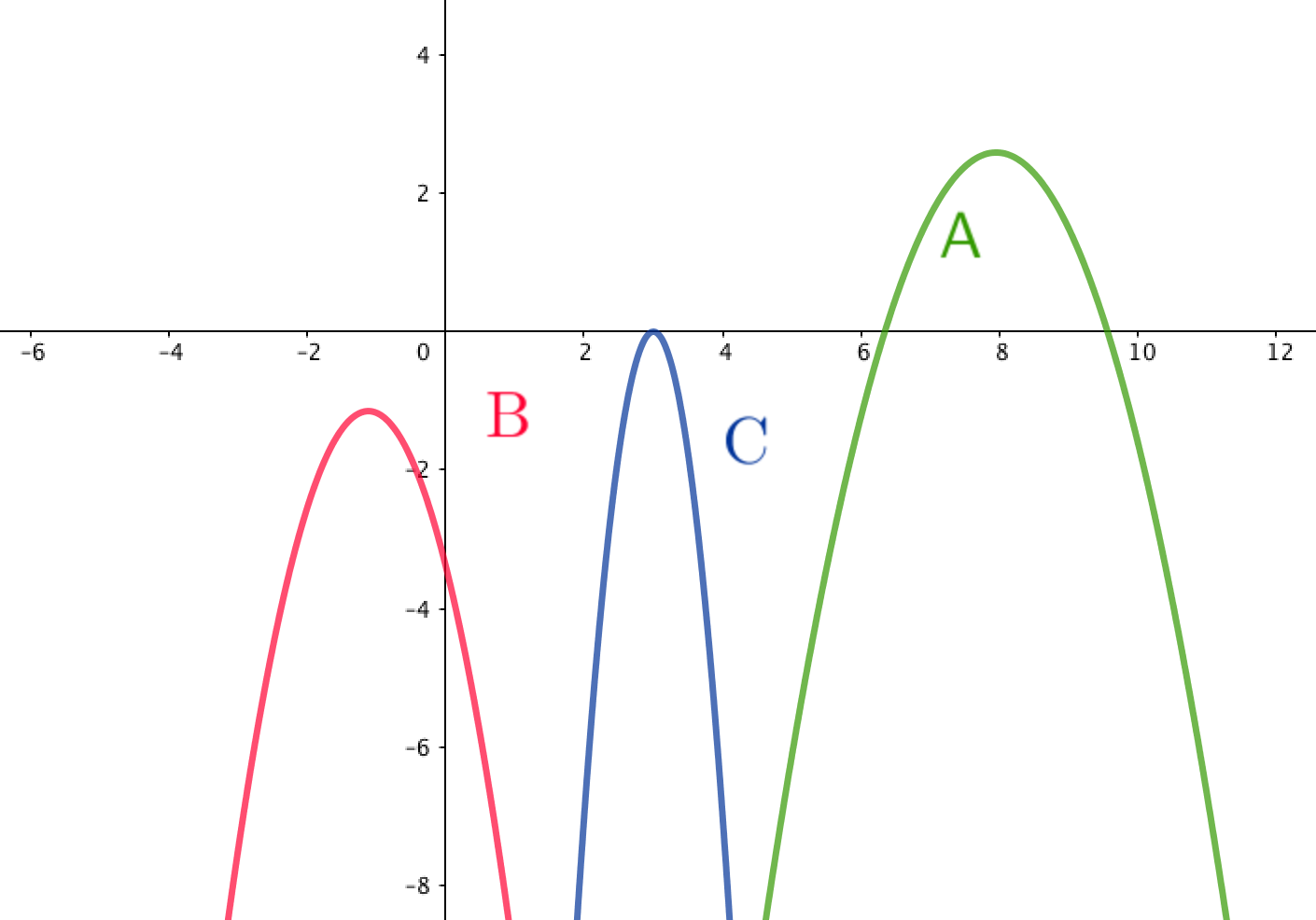
Выберите квадратичную функцию с отрицательным дискриминантом.
Определим на параболе \(\displaystyle y=ax^2+bx+c\) точки, которые являются корнями квадратного уравнения \(\displaystyle ax^2+bx+c=0 {\small .} \)
Поскольку \(\displaystyle ax^2+bx+c=0{ \small ,} \) то это точки на параболе, для которых \(\displaystyle y=0{ \small .} \) Точки, у которых \(\displaystyle y=0{ \small ,} \) лежат также на оси \(\displaystyle \rm OX{\small .} \)
То есть, с одной стороны, точки лежат на параболе, а с другой – на оси \(\displaystyle \rm OX{\small .} \) Значит, это точки пересечения параболы с осью \(\displaystyle \rm OX {\small .}\)
Перечислим возможные случаи:
| Число точек пересечения параболы с осью \(\displaystyle \rm OX \) | Число корней квадратного уравнения |
| Две точки пересечения | Два решения |
| Одна точка пересечения (касание оси) | Одно решение |
| Нет точек пересечения | Нет решений |
Или, формулируя через дискриминант:
| Число точек пересечения параболы с осью \(\displaystyle \rm OX \) | Знак дискриминанта \(\displaystyle \rm D \) |
| Две точки пересечения | \(\displaystyle {\rm D}>0 \) |
| Одна точка пересечения (касание оси) | \(\displaystyle {\rm D}=0 \) |
| Нет точек пересечения | \(\displaystyle {\rm D}<0 \) |
Найдем на рисунке из условия задачи квадратичные функции с отрицательным дискриминантом.
Это те параболы, у которых нет точек пересечения с осью \(\displaystyle \rm OX{\small . } \)

Точек пересечения с осью \(\displaystyle \rm OX \) не имеет только парабола \(\displaystyle \rm \color{red}{ B}{\small .} \)
Ответ: \(\displaystyle \rm \color{red}{ B}{\small .} \)