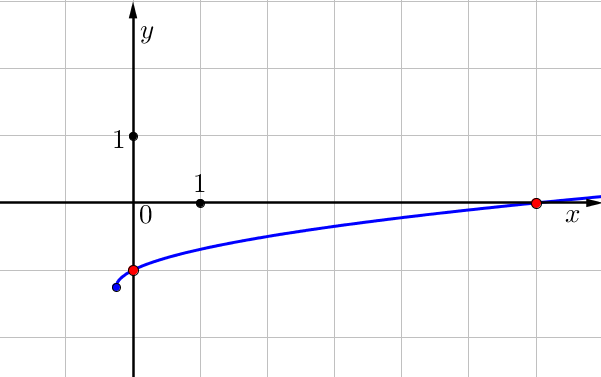
На рисунке изображён график функции \(\displaystyle f\left(x\right)=k\sqrt{x+b}-\frac{5}{4} \small.\) Найдите значение \(\displaystyle x \small,\) при котором \(\displaystyle f\left(x\right)=\frac{5}{4} \small.\)
\(\displaystyle x=\)
Чтобы найти значение \(\displaystyle x\small,\) при котором \(\displaystyle f\left(x\right)=\frac{5}{4} \small,\)
- найдем неизвестные коэффициенты \(\displaystyle \color{blue}b\) и \(\displaystyle \color{orange}k\small,\)
- решим уравнение \(\displaystyle \color{orange}k \cdot \sqrt{x+\color{blue}b}-\frac{5}{4}=\frac{5}{4}\small.\)
Обозначим отмеченные точки на графике функции \(\displaystyle f\left(x\right)=\color{orange}{k}\sqrt{x+\color{blue}b}-\frac{5}{4}\) буквами \(\displaystyle \color{red}A\) и \(\displaystyle \color{Magenta}B \small.\)
Определим координаты этих точек:
- \(\displaystyle x_1=\color{red}{0}\) – абсцисса, \(\displaystyle y_1=\color{red}{-1}\) – ордината точки \(\displaystyle \color{red}A\small,\)
- \(\displaystyle x_2=\color{Magenta}{6}\) – абсцисса, \(\displaystyle y_2=\color{Magenta}{0}\) – ордината точки \(\displaystyle \color{Magenta}B\small.\)
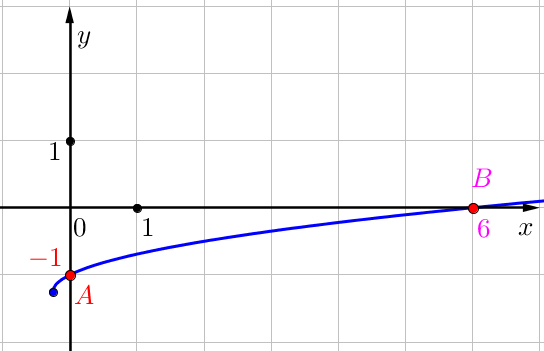
Точки \(\displaystyle \color{red}{A(0;-1)}\) и \(\displaystyle \color{Magenta}{B(6;0)}\) лежат на графике функции \(\displaystyle f\left(x\right)=\color{orange}{k}\sqrt{x+\color{blue}b}-\frac{5}{4}\small.\)
Значит,
- при подстановке \(\displaystyle x=\color{red}{0}\) и \(\displaystyle y=\color{red}{-1}\) в уравнение \(\displaystyle y=\color{orange}{k}\sqrt{x+\color{blue}{b}}-\frac{5}{4}\) получим первое верное равенство,
- при подстановке \(\displaystyle x=\color{Magenta}{6}\) и \(\displaystyle y=\color{Magenta}{0}\) в уравнение \(\displaystyle y=\color{orange}{k}\sqrt{x+\color{blue}{b}}-\frac{5}{4}\) получим второе верное равенство.
В итоге получаем систему уравнений:
\(\displaystyle\left\{\begin{aligned}\color{red}{-1}&=\color{orange}{k} \cdot \sqrt{\color{red}{0}+\color{blue}{b}}-\frac{5}{4}{\small,} \\[10px]\color{Magenta}{0}&=\color{orange}{k} \cdot \sqrt{\color{Magenta}{6}+\color{blue}{b}}-\frac{5}{4}{\small.}\end{aligned}\right.\)
Таким образом, исходная функция имеет вид:
\(\displaystyle f\left(x\right)=\color{orange}{\frac{1}{2}}\sqrt{x+\color{blue}{\frac{1}{4}}}-\frac{5}{4} \small.\)
\(\displaystyle x=24{,}75 \small.\)
Ответ:\(\displaystyle 24{,}75 \small.\)