Какие из следующих утверждений верны?
\(\displaystyle 1)\) Все медианы равностороннего треугольника равны.
\(\displaystyle 2)\) Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу.
\(\displaystyle 3)\) В любой ромб можно вписать окружность.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Рассмотрим каждое утверждение:
\(\displaystyle 1)\) Все медианы равностороннего треугольника равны.
| Равносторонний треугольник – это треугольник, у которого все стороны равны между собой по длине, все углы также равны и составляют \(\displaystyle 60^{\circ} {\small.}\) | 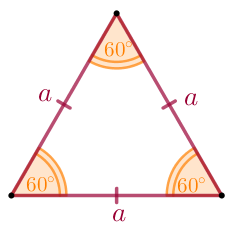 |
Свойство равностороннего треугольника
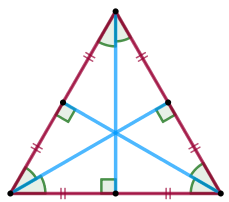 | В равностороннем треугольнике медиана, проведенная к каждой стороне, является биссектрисой и высотой, и они равны между собой. |
\(\displaystyle 2)\) Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу.
Центральный и вписанный угол
| Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. | 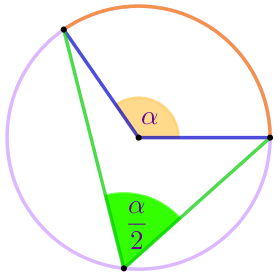 |
\(\displaystyle 3)\) В любой ромб можно вписать окружность.
Признак описанного четырёхугольника
Если суммы длин противоположных сторон четырехугольника равны, то в него можно вписать окружность.
Если \(\displaystyle \color{blue}{AB}+\color{blue}{CD}=\color{red}{BC}+\color{red}{AD}{\small,}\) то \(\displaystyle ABCD\) – описанный. |
| Ромб – это параллелограмм, у которого все стороны равны. | 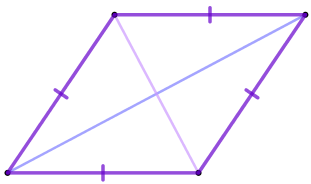 |
Следовательно, суммы противоположных сторон ромба равны. Значит, в любой ромб можно вписать окружность.
Ответ: \(\displaystyle 13 {\small.}\)