Какое из следующих утверждений верно?
\(\displaystyle 1)\) Все равнобедренные треугольники подобны.
\(\displaystyle 2)\) Существует прямоугольник, диагонали которого взаимно перпендикулярны.
\(\displaystyle 3)\) Сумма углов прямоугольного треугольника равна \(\displaystyle 90\) градусам.
В ответ запишите номер выбранного утверждения.
Рассмотрим каждое утверждение:
\(\displaystyle 1)\) Все равнобедренные треугольники подобны.
Подобные треугольники
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.
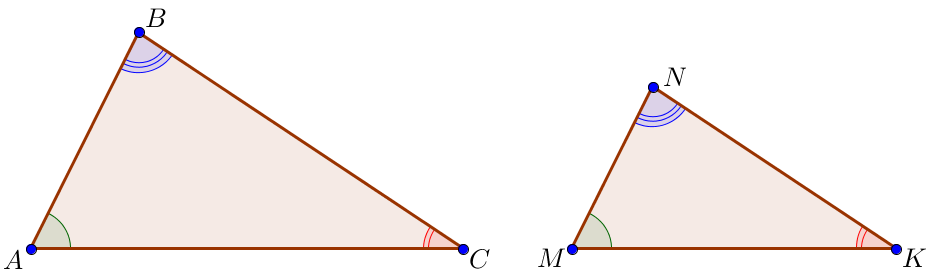
\(\displaystyle \triangle ABC \sim \triangle MNK\small: \)
\(\displaystyle \angle A = \angle M \small, \) \(\displaystyle \angle B = \angle N \small, \) \(\displaystyle \angle C = \angle K \small, \)
\(\displaystyle \frac{AB}{MN} = \frac{BC}{NK} = \frac{AC}{MK} \small. \)
Пример.
Равнобедренные остроугольный и тупоугольный треугольники не подобны.
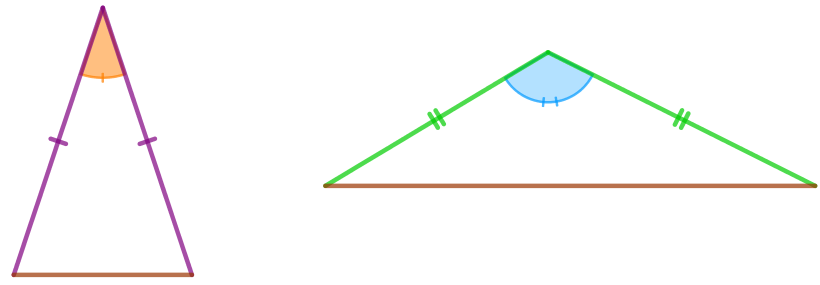
Следовательно, утверждение \(\displaystyle 1) \) неверно.
\(\displaystyle 2)\) Существует прямоугольник, диагонали которого взаимно перпендикулярны.
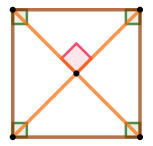 | Прямоугольник, диагонали которого взаимно перпендикулярны – это квадрат. |
\(\displaystyle 3)\) Сумма углов прямоугольного треугольника равна \(\displaystyle 90\) градусам.
Сумма углов треугольника равна \(\displaystyle 180^{\circ}{\small.}\)
| \(\displaystyle \color{red}{\alpha}+\color{green}{\beta}+\color{blue}{\gamma}=180^{\circ}\) |
Чтобы утверждение стало верным, его следует сформулировать так:
Сумма острых углов прямоугольного треугольника равна \(\displaystyle 90\) градусам.
Ответ: \(\displaystyle 2 {\small.}\)