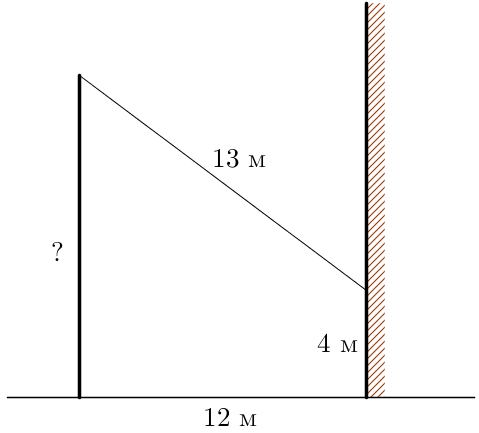
От столба к дому натянут провод длиной \(\displaystyle 13\)м, который закреплён на стене дома на высоте \(\displaystyle 4\)м от земли (см. рис.). Найдите высоту столба, если расстояние от дома до столба \(\displaystyle 12\)м. Ответ дайте в метрах.
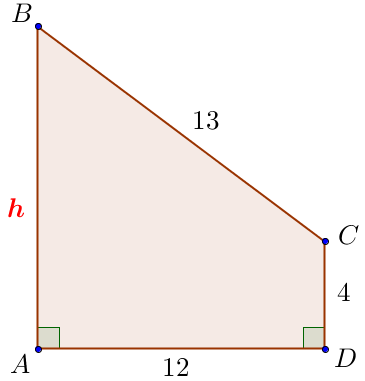
Пусть \(\displaystyle h\) – высота столба. Изобразим предложенную в задаче конструкцию в виде прямоугольной трапеции \(\displaystyle ABCD \small, \) в которой: \(\displaystyle \angle A =90^{\circ} \small, \) \(\displaystyle \angle D =90^{\circ} \small, \) \(\displaystyle AB=h \small, \) \(\displaystyle AD=12 \small, \) \(\displaystyle CD=4 \small, \) \(\displaystyle BC=13 \small. \)
|  |
Из точки \(\displaystyle C\) к стороне \(\displaystyle AB\) опустим перпендикуляр \(\displaystyle CH \small. \)
\(\displaystyle AHCD\) – прямоугольник. Противоположные стороны прямоугольника равны. Значит, \(\displaystyle HC=AD=12 \small, \) \(\displaystyle AH=CD=4\small. \) Тогда \(\displaystyle AB=BH+AH \small, \) \(\displaystyle h=BH+4\small. \) | 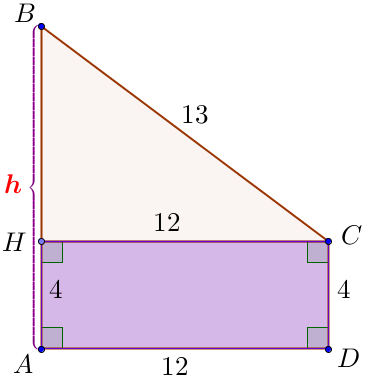 |
Найдем длину отрезка \(\displaystyle BH\small. \)
Рассмотрим прямоугольный треугольник \(\displaystyle BHC \small. \)
По теореме Пифагора \(\displaystyle BC^2=BH^2+HC^2 {\small,} \) \(\displaystyle BH^2=BC^2-HC^2 {\small,} \) \(\displaystyle BH^2=13^2-12^2=169-144=25{\small,} \) \(\displaystyle BH= \pm \sqrt{25}=\pm 5 \small. \) Так как \(\displaystyle BH\) – катет прямоугольного треугольника \(\displaystyle BHC \small, \) то \(\displaystyle BH>0 \small. \) Значит, \(\displaystyle BH=5\small. \) | 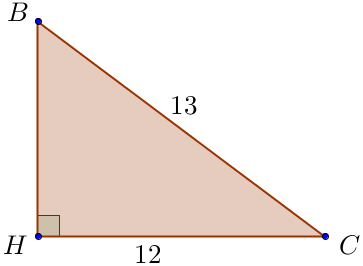 |
Найдем высоту столба:
\(\displaystyle h=BH+4\small, \)
\(\displaystyle h=5+4=9 \small. \)
Высота столба равна \(\displaystyle 9\) метров.
Ответ: \(\displaystyle 9 \small. \)