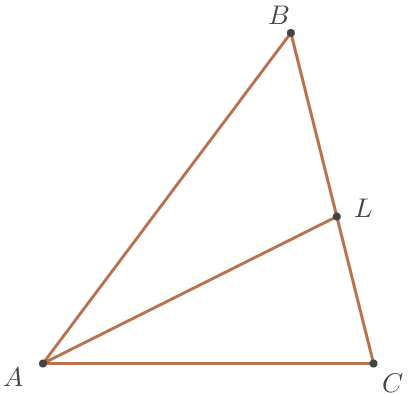
В треугольнике \(\displaystyle ABC\) проведена биссектриса \(\displaystyle AL{\small,}\) угол \(\displaystyle ALC\) равен \(\displaystyle 76^{\circ} {\small,}\) угол \(\displaystyle ABC\) равен \(\displaystyle 47^{\circ}{\small.}\) Найдите угол \(\displaystyle ACB{\small.}\) Ответ дайте в градусах.
Пусть \(\displaystyle \angle ACB=\color{red}{x} {\small.}\) По условию \(\displaystyle \angle ALC=76^{\circ} \) и \(\displaystyle \angle ABC=47^{\circ} {\small.}\) Так как \(\displaystyle AL\) – биссектриса угла \(\displaystyle BAC {\small,}\) то \(\displaystyle \angle BAL=\angle CAL=\alpha {\small.}\) Поскольку сумма внутренних углов треугольника равна \(\displaystyle 180^{\circ} {\small,}\) то в треугольнике \(\displaystyle ALC \) угол \(\displaystyle \color{red}x \) равен \(\displaystyle \color{red}x= 180^{\circ}-76^{\circ}- \alpha {\small,}\) \(\displaystyle \color{red}x= 104^{\circ}- \alpha {\small.}\) | 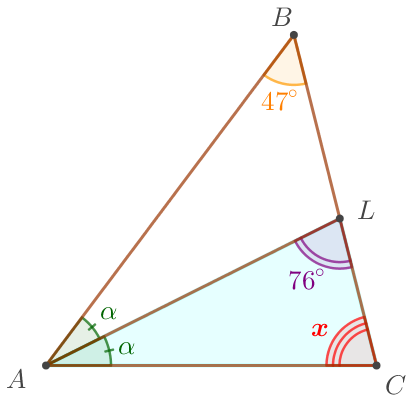 |
Найдём угол \(\displaystyle \alpha \) из треугольника \(\displaystyle ABL {\small.}\)
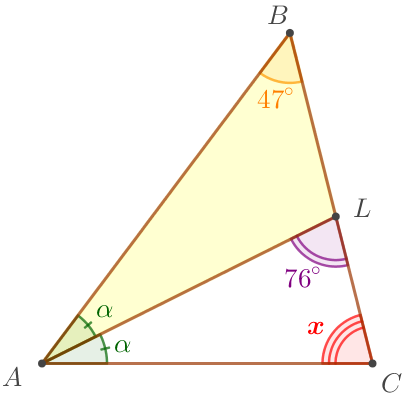 | Заметим, что \(\displaystyle \angle ALC \) – внешний угол треугольника \(\displaystyle ABL {\small.}\) Так как внешний угол треугольника равен сумме двух углов не смежных с ним, то \(\displaystyle 76^{\circ}=\alpha+47^{\circ} {\small.}\) Тогда \(\displaystyle \alpha=76^{\circ}-47^{\circ} = 29^{\circ}{\small.}\) Получаем \(\displaystyle \color{red}x= 104^{\circ}-29^{\circ}=75^{\circ} {\small.}\) |
Ответ: \(\displaystyle 75 {\small.} \)