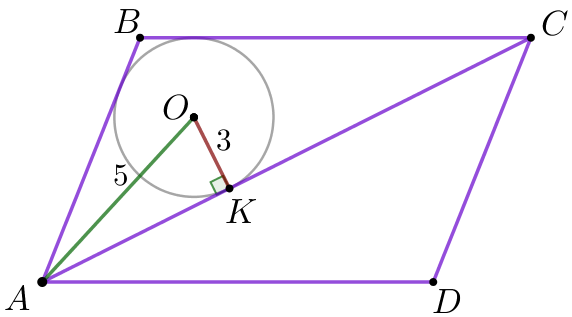
В параллелограмме \(\displaystyle ABCD\) проведена диагональ \(\displaystyle AC {\small.}\) Точка \(\displaystyle O\) является центром окружности, вписанной в треугольник \(\displaystyle ABC {\small.}\) Расстояние от точки \(\displaystyle O\) до точки \(\displaystyle A\) и прямой \(\displaystyle AC\) соответственно равны \(\displaystyle 5\) и \(\displaystyle 3{\small.}\) Найдите длину стороны \(\displaystyle BC{\small,}\) если площадь параллелограмма \(\displaystyle ABCD \) равна \(\displaystyle 168{\small.}\)
По условию задачи выполним построения.
Пусть \(\displaystyle ABCD\) – параллелограмм, \(\displaystyle AC\) – диагональ параллелограмма,
\(\displaystyle O\)– центр окружности, вписанной в треугольник \(\displaystyle ABC {\small.}\)
 |
|
Требуется найти длину стороны \(\displaystyle BC{\small.}\)
Обозначим буквами \(\displaystyle M\) и \(\displaystyle N\) – точки касания окружности со сторонами \(\displaystyle AB\) и \(\displaystyle BC\) соответственно. Отрезки \(\displaystyle OM {\small,}\) \(\displaystyle ON\) и \(\displaystyle OK\) равны как радиусы вписанной окружности. То есть \(\displaystyle OM=ON=OK=3 {\small.}\) Пусть \(\displaystyle BN=x {\small,}\) \(\displaystyle CN=y {\small.}\) Тогда \(\displaystyle BC=x+y{\small.}\) | 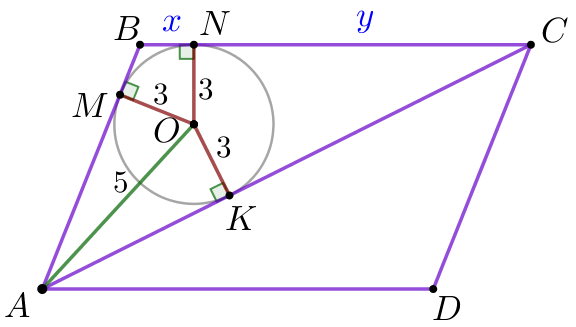 |
Диагональ \(\displaystyle AC\) делит параллелограмм \(\displaystyle ABCD\) на два равных треугольника:
\(\displaystyle \triangle ABC= \triangle ADC\) (по трём сторонам).
Следовательно,
\(\displaystyle S_{\triangle ABC}= \frac{1}{2} \cdot S_{ABCD} {\small;}\)
\(\displaystyle S_{\triangle ABC}= \frac{1}{2} \cdot 168=84 {\small.}\)
Рассмотрим треугольник \(\displaystyle ABC{\small.}\)
Поскольку отрезки касательных к окружности, проведенных из одной точки, равны, то
\(\displaystyle BN=BM=x {\small,}\) \(\displaystyle CN=CK=y \) и \(\displaystyle AM=AK{\small.}\)
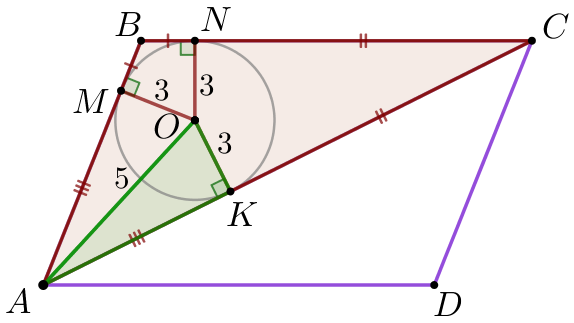 | Длину отрезка \(\displaystyle AK\) найдем из прямоугольного треугольника \(\displaystyle AOK\) по теореме Пифагора: \(\displaystyle AK^2=AO^2-OK^2 {\small;}\) \(\displaystyle AK^2=5^2-3^2 =25-9=16=4^2{\small.}\) Так как длина отрезка не может быть отрицательной, то \(\displaystyle AK=4{\small.}\) |
Запишем длины сторон \(\displaystyle \triangle ABC {\small:}\) \(\displaystyle BC=x+y{\small,}\) \(\displaystyle AB=x+4{\small,}\) \(\displaystyle AC=y+4{\small.}\) Периметр треугольника равен сумме длин всех сторон: \(\displaystyle P_{\triangle ABC}=BC+AB+AC{\small;}\) \(\displaystyle P_{\triangle ABC}=x+y+x+4+y+4=2 \cdot (x+y+4){\small.}\) | 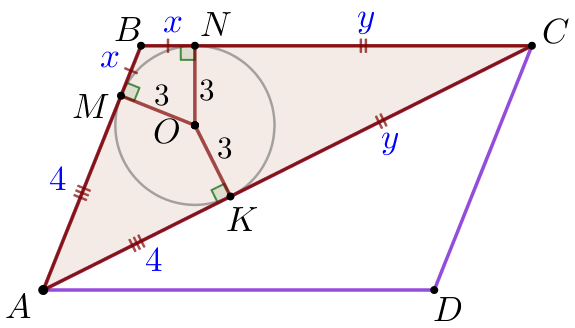 |
Учитывая, что \(\displaystyle x+y=BC{\small,}\) получаем
\(\displaystyle P_{\triangle ABC}=2 \cdot (BC+4){\small.}\)
Выразим площадь треугольника через периметр и радиус вписанной окружности:
\(\displaystyle S_{\triangle ABC}=\frac{1}{2} \cdot P_{\triangle ABC} \cdot r{\small;}\)
\(\displaystyle r=OK=3{\small;}\)
\(\displaystyle S_{\triangle ABC}=\frac{1}{\cancel{2}} \cdot \cancel{2} \cdot (BC+4) \cdot 3=3\cdot BC+12{\small.}\)
Так как
\(\displaystyle S_{\triangle ABC}=84\) и \(\displaystyle S_{\triangle ABC}=3\cdot BC+12{\small,}\)
то
\(\displaystyle 84=3\cdot BC+12{\small;}\)
\(\displaystyle 3\cdot BC=72 {\small;}\)
\(\displaystyle BC=24 {\small.}\)
Ответ: \(\displaystyle 24{\small.}\)