Окружность с центром на стороне \(\displaystyle AC\) треугольника \(\displaystyle ABC\) проходит через вершину \(\displaystyle C\) и касается прямой \(\displaystyle AB\) в точке \(\displaystyle B {\small.}\) Найдите \(\displaystyle AC {\small,}\) если диаметр окружности равен \(\displaystyle 16 {\small,}\) а \(\displaystyle AB=15 {\small.}\)
Выполним чертёж по условию задачи.
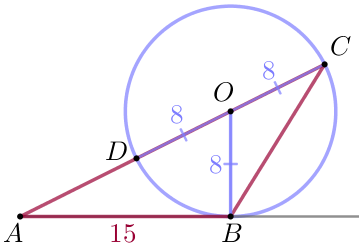 | Точка \(\displaystyle O\) лежит на стороне \(\displaystyle AC\) треугольника \(\displaystyle ABC {\small.}\) Окружность с центром в точке \(\displaystyle O\) проходит через вершины \(\displaystyle C\) и \(\displaystyle B\) данного треугольника. Буквой \(\displaystyle D\) обозначим точку, в которой эта окружность пересекает сторону \(\displaystyle AC {\small.}\) \(\displaystyle CD=16\) – диаметр окружности, \(\displaystyle AB=15 {\small.}\) \(\displaystyle OD=OC=OB=\frac{1}{2} \cdot 16=8 \) – радиусы окружности. |
Способ решения 1
Рассмотрим треугольник \(\displaystyle AOB {\small.}\)
По теореме Пифагора \(\displaystyle AO^2=AB^2+OB^2 {\small,}\) \(\displaystyle AO^2=15^2+8^2 {\small,}\) \(\displaystyle AO^2=225+64=289=17^2 {\small.}\) Так как длина отрезка не может быть отрицательной, то \(\displaystyle AO=17{\small.}\) | 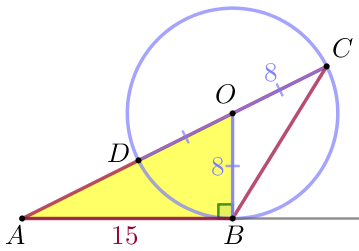 |
Длина отрезка \(\displaystyle AC\) равна сумме длин отрезков \(\displaystyle AO\) и \(\displaystyle OC {\small:}\)
\(\displaystyle AC=AO+OC {\small,}\)
\(\displaystyle AC=17+8=25{\small.}\)
Ответ: \(\displaystyle 25 {\small.}\)
Способ решения 2
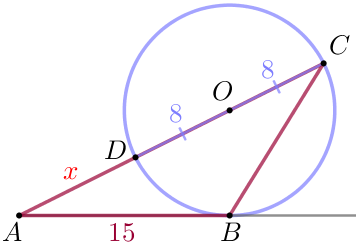 | \(\displaystyle AB^2=AC \cdot AD {\small,}\) где:
|
Подставляя, получаем:
\(\displaystyle 15^2=(x+16) \cdot x {\small,}\)
\(\displaystyle 225=x^2+16x {\small,}\)
\(\displaystyle x^2+16x-225=0{\small.}\)
Так как длина отрезка не может быть отрицательной, то \(\displaystyle x=9{\small.}\)
Тогда
\(\displaystyle AC=x+16=9+16=25 {\small.}\)
Ответ: \(\displaystyle 25 {\small.}\)