Синус мәндері \(\displaystyle \rm OY{ \small}\) осьте орналасқандықтан \(\displaystyle y=-\frac{\sqrt{3}}{2}\) түзуді және тригонометриялық шеңберді кесіп өтеміз:
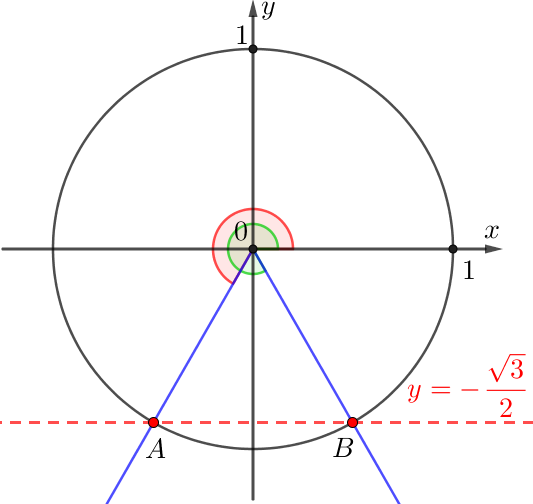
Біз екі нүктеге сәйкес шешімдердің екі жиынтығын аламыз.
\(\displaystyle A{\small}\) нүктесіне сәйкес келетін сәуленің айналу бұрышы \(\displaystyle \frac{4\pi}{3}\) радианға тең.
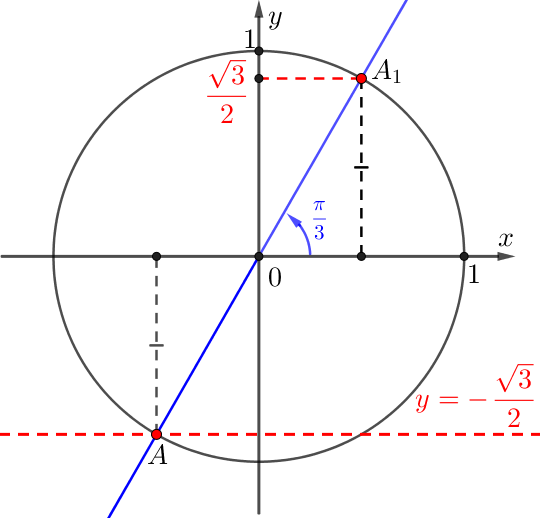
Тригонометриялық функциялардың мәндер кестесіне сәйкес \(\displaystyle \sin\left(\frac{\pi}{3}\right)=\frac{\sqrt{3}}{2}{\small.}\)
\(\displaystyle A\) нүктесі \(\displaystyle A_1{\small}\) бұрылуына сәйкес \(\displaystyle \frac{\pi}{3}{\small}\) нүктесіне орталық симметриялы:
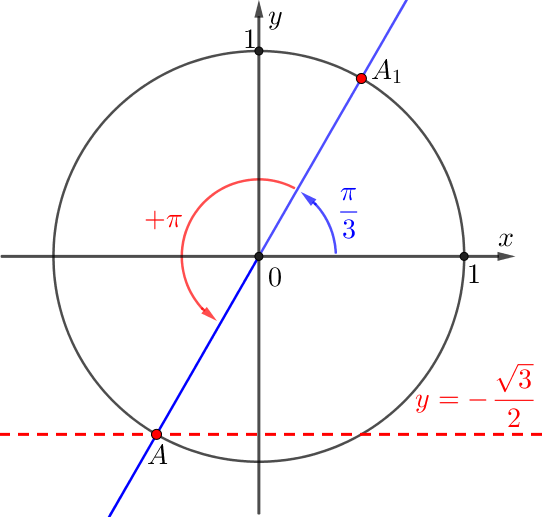
Демек, \(\displaystyle OA\) сәуленің айналу бұрышы \(\displaystyle \pi+\frac{\pi}{3}=\frac{4\pi}{3}{\small}\) тең:
Осылайша, шешімдердің бірінші жиынтығын аламыз:
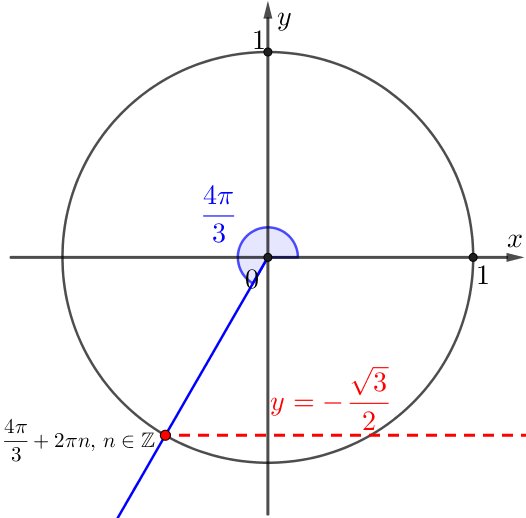 | \(\displaystyle x_1=\frac{4\pi}{3}+2\pi n, \, n\in \mathbb{Z}{ \small .}\) |
\(\displaystyle B{\small}\) нүктесіне сәйкес сәуленің айналу бұрышы \(\displaystyle \frac{5\pi}{3}\) радианға тең.
Тригонометриялық функциялардың мәндер кестесіне сәйкес \(\displaystyle \sin\left(\frac{\pi}{3}\right)=\frac{\sqrt{3}}{2}{\small.}\)
\(\displaystyle B\) нүктесі \(\displaystyle \rm OX\) оське қатысты \(\displaystyle B_1{\small}\) бойынша айналуға сәйкес келетін \(\displaystyle \frac{\pi}{3}{\small}\) нүктесіне симметриялы.
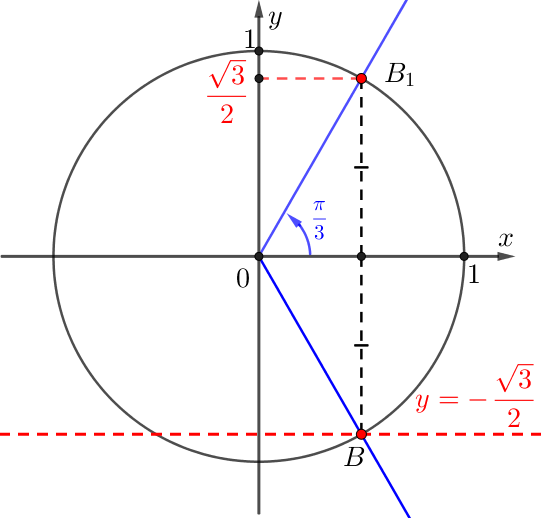
Демек, \(\displaystyle OB\) сәуленің айналу бұрышы \(\displaystyle -\frac{\pi}{3}\) немесе \(\displaystyle 2\pi-\frac{\pi}{3}=\frac{5\pi}{3}{\small}\) тең:
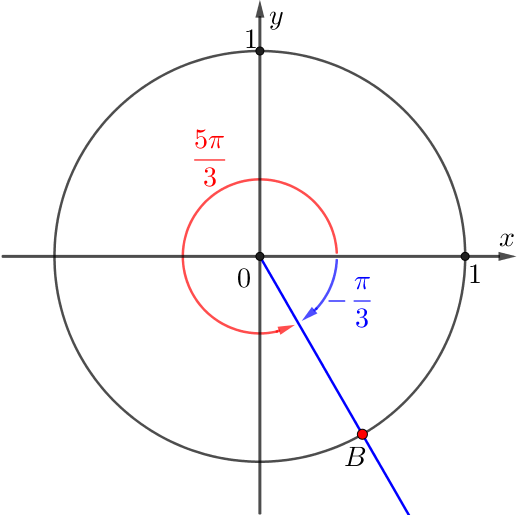
Осылайша, шешімдердің екінші жиынтығын аламыз:
 | \(\displaystyle x_1=\frac{5\pi}{3}+2\pi n, \, n\in \mathbb{Z}{ \small .}\)
|
Жауабы: \(\displaystyle x_1=\frac{4\pi}{3}+2\pi n, \, n\in \mathbb{Z}\) және \(\displaystyle x_2=\frac{5\pi}{3}+2\pi n, \, n\in \mathbb{Z}{ \small .}\)