Skip to main content

Теориясы: 09 Тригонометриялық функциялар

Тапсырма

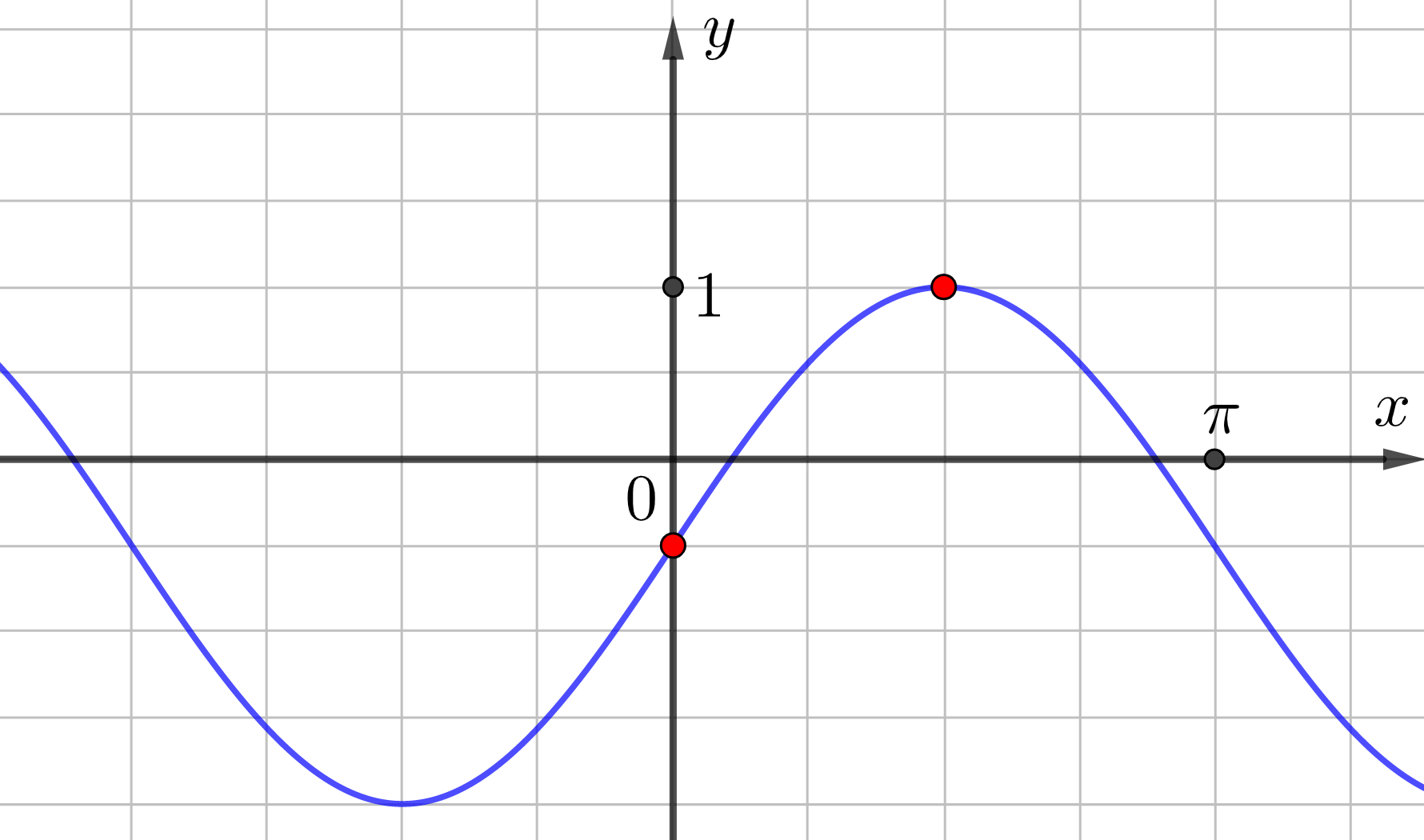
Суретте \(\displaystyle f\left(x\right)=a\sin x +b{\small}\) функцияның графигі көрсетілген. \(\displaystyle f\bigg(\frac{\pi}{6}\bigg){\small}\) табыңыз.  

   


\(\displaystyle f\bigg(\frac{\pi}{6}\bigg)=\)

Шешім

\(\displaystyle f\bigg(\frac{\pi}{6}\bigg){\small}\) табу үшін, алдымен белгісіз \(\displaystyle a\) және \(\displaystyle b\) коэффициенттерін табамыз.     

Ол үшін \(\displaystyle a\) және \(\displaystyle b\) қатысты теңдеулер жүйесін құрамыз және оны шешеміз.  

\(\displaystyle f(x)=a\sin x +b{ \small}\) функциясының графигінде белгіленген нүктелер \(\displaystyle \Big(\color{blue}{0};\color{blue}{-\frac{1}{2}}\Big)\) және \(\displaystyle \Big(\color{green}{\frac{\pi}{2}};\color{green}{1}\Big){\small}\) координаталарына ие екендігін ескереміз.               

 

Демек,

  • \(\displaystyle x=\color{blue}{0}\) және \(\displaystyle y=\color{blue}{-\frac{1}{2}}\)  координаталарын \(\displaystyle y=a\sin x +b\) теңдеуіне қойғанда дұрыс теңдік аламыз;                             
  • \(\displaystyle x=\color{green}{\frac{\pi}{2}}\) және \(\displaystyle y=\color{green}{1}\)  координаталарын \(\displaystyle y=a\sin x +b\) теңдеуіне қойғанда дұрыс теңдік аламыз.     

Осылайша, теңдеулер жүйесін аламыз:  

\(\displaystyle \left\{\begin{aligned}\color{blue}{-\frac{1}{2}}&=a\cdot \sin \color{blue}{0}+b{ \small ,}\\\color{green}{1}&=a\cdot \sin\color{green}{\frac{\pi}{2}}+b{ \small .}\end{aligned}\right. \)

\(\displaystyle \sin \color{blue}{0}\) және \(\displaystyle \sin\color{green}{\frac{\pi}{2}}\) орнына олардың мәнін қоямыз.    

\(\displaystyle \sin{0}=0\) 

\(\displaystyle \sin \frac{\pi}{2}=1\) 

Қою арқылы келесіні аламыз:

\(\displaystyle \left\{\begin{aligned}{-\frac{1}{2}}&=a\cdot 0+b{ \small ,}\\{1}&=a\cdot1+b\end{aligned}\right. \)

немесе

\(\displaystyle \left\{\begin{aligned}{-\frac{1}{2}}&=b{ \small ,}\\{1}&=a+b{ \small .}\end{aligned}\right. \)

Алынған теңдеулер жүйесін шешейік.

Берілген теңдеулер жүйесінің шешімі \(\displaystyle a=\frac{3}{2}\) және \(\displaystyle b=-\frac{1}{2}\)

Сонда бастапқы функция келесідей болады:

\(\displaystyle f(x)=\frac{3}{2}\sin x -\frac{1}{2}{ \small .}\) 

\(\displaystyle f\bigg(\frac{\pi}{6}\bigg){ \small}\) табамыз:

\(\displaystyle f\bigg(\frac{\pi}{6}\bigg)=\frac{3}{2}\cdot \sin \frac{\pi}{6} -\frac{1}{2}{ \small .}\) 

\(\displaystyle \sin \frac{\pi}{6} \)мәні – кестелік. Оны ауыстырамыз:

Кеңес – кестелік мәндер

\(\displaystyle f\bigg(\frac{\pi}{6}\bigg)=\frac{3}{2}\cdot \sin \frac{\pi}{6} -\frac{1}{2}= \frac{3}{2}\cdot \frac{1}{2} -\frac{1}{2}=\frac{3}{4}-\frac{2}{4}=\frac{1}{4}=0{,}25{\small.}\)

Жауабы: \(\displaystyle f\bigg(\frac{\pi}{6}\bigg)=0{,}25{\small.}\)